Welcome to Subscribe On Youtube
515. Find Largest Value in Each Tree Row
Description
Given the root of a binary tree, return an array of the largest value in each row of the tree (0-indexed).
Example 1:
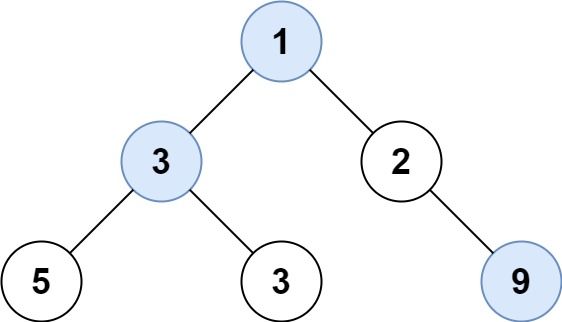
Input: root = [1,3,2,5,3,null,9] Output: [1,3,9]
Example 2:
Input: root = [1,2,3] Output: [1,3]
Constraints:
- The number of nodes in the tree will be in the range
[0, 104]. -231 <= Node.val <= 231 - 1
Solutions
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public List<Integer> largestValues(TreeNode root) { List<Integer> ans = new ArrayList<>(); if (root == null) { return ans; } Deque<TreeNode> q = new ArrayDeque<>(); q.offer(root); while (!q.isEmpty()) { int t = q.peek().val; for (int i = q.size(); i > 0; --i) { TreeNode node = q.poll(); t = Math.max(t, node.val); if (node.left != null) { q.offer(node.left); } if (node.right != null) { q.offer(node.right); } } ans.add(t); } return ans; } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: vector<int> largestValues(TreeNode* root) { if (!root) return {}; queue<TreeNode*> q{ {root} }; vector<int> ans; while (!q.empty()) { int t = q.front()->val; for (int i = q.size(); i; --i) { TreeNode* node = q.front(); t = max(t, node->val); q.pop(); if (node->left) q.push(node->left); if (node->right) q.push(node->right); } ans.push_back(t); } return ans; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def largestValues(self, root: Optional[TreeNode]) -> List[int]: if root is None: return [] q = deque([root]) ans = [] while q: t = -inf for _ in range(len(q)): node = q.popleft() t = max(t, node.val) if node.left: q.append(node.left) if node.right: q.append(node.right) ans.append(t) return ans -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func largestValues(root *TreeNode) []int { var ans []int if root == nil { return ans } q := []*TreeNode{root} for len(q) > 0 { t := q[0].Val for i := len(q); i > 0; i-- { node := q[0] q = q[1:] t = max(t, node.Val) if node.Left != nil { q = append(q, node.Left) } if node.Right != nil { q = append(q, node.Right) } } ans = append(ans, t) } return ans } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function largestValues(root: TreeNode | null): number[] { const res: number[] = []; const queue: TreeNode[] = []; if (root) { queue.push(root); } while (queue.length) { const n = queue.length; let max = -Infinity; for (let i = 0; i < n; i++) { const { val, left, right } = queue.shift(); max = Math.max(max, val); left && queue.push(left); right && queue.push(right); } res.push(max); } return res; } -
// Definition for a binary tree node. // #[derive(Debug, PartialEq, Eq)] // pub struct TreeNode { // pub val: i32, // pub left: Option<Rc<RefCell<TreeNode>>>, // pub right: Option<Rc<RefCell<TreeNode>>>, // } // // impl TreeNode { // #[inline] // pub fn new(val: i32) -> Self { // TreeNode { // val, // left: None, // right: None // } // } // } use std::rc::Rc; use std::cell::RefCell; use std::collections::VecDeque; impl Solution { pub fn largest_values(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> { let mut res = Vec::new(); let mut queue = VecDeque::new(); if root.is_some() { queue.push_back(root.clone()); } while !queue.is_empty() { let mut max = i32::MIN; for _ in 0..queue.len() { let node = queue.pop_front().unwrap(); let node = node.as_ref().unwrap().borrow(); max = max.max(node.val); if node.left.is_some() { queue.push_back(node.left.clone()); } if node.right.is_some() { queue.push_back(node.right.clone()); } } res.push(max); } res } }