Welcome to Subscribe On Youtube

510. Inorder Successor in BST II

Description

Given a node in a binary search tree, return the in-order successor of that node in the BST. If that node has no in-order successor, return null.

The successor of a node is the node with the smallest key greater than node.val.

You will have direct access to the node but not to the root of the tree. Each node will have a reference to its parent node. Below is the definition for Node:

class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

 

Example 1:

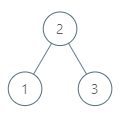
Input: tree = [2,1,3], node = 1
Output: 2
Explanation: 1's in-order successor node is 2. Note that both the node and the return value is of Node type.

Example 2:

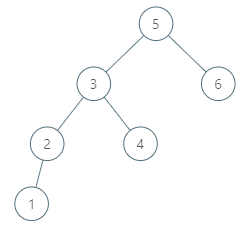
Input: tree = [5,3,6,2,4,null,null,1], node = 6
Output: null
Explanation: There is no in-order successor of the current node, so the answer is null.

 

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -105 <= Node.val <= 105
• All Nodes will have unique values.

 

Follow up: Could you solve it without looking up any of the node's values?

Solutions

• Java
• C++
• Python
• Go
• Javascript
• TypeScript

• /*
  // Definition for a Node.
  class Node {
      public int val;
      public Node left;
      public Node right;
      public Node parent;
  };
  */
  
  class Solution {
      public Node inorderSuccessor(Node node) {
          if (node.right != null) {
              node = node.right;
              while (node.left != null) {
                  node = node.left;
              }
              return node;
          }
          while (node.parent != null && node == node.parent.right) {
              node = node.parent;
          }
          return node.parent;
      }
  }
  

• /*
  // Definition for a Node.
  class Node {
  public:
      int val;
      Node* left;
      Node* right;
      Node* parent;
  };
  */
  
  class Solution {
  public:
      Node* inorderSuccessor(Node* node) {
          if (node->right) {
              node = node->right;
              while (node->left) node = node->left;
              return node;
          }
          while (node->parent && node == node->parent->right) node = node->parent;
          return node->parent;
      }
  };
  

• """
  # Definition for a Node.
  class Node:
      def __init__(self, val):
          self.val = val
          self.left = None
          self.right = None
          self.parent = None
  """
  
  
  class Solution:
      def inorderSuccessor(self, node: 'Node') -> 'Optional[Node]':
          if node.right:
              node = node.right
              while node.left:
                  node = node.left
              return node
          while node.parent and node == node.parent.right:
              node = node.parent
          return node.parent
  
  

• /**
   * Definition for Node.
   * type Node struct {
   *     Val int
   *     Left *Node
   *     Right *Node
   *     Parent *Node
   * }
   */
  
  func inorderSuccessor(node *Node) *Node {
  	if node.Right != nil {
  		node = node.Right
  		for node.Left != nil {
  			node = node.Left
  		}
  		return node
  	}
  	for node.Parent != nil && node == node.Parent.Right {
  		node = node.Parent
  	}
  	return node.Parent
  }
  

• /**
   * // Definition for a Node.
   * function Node(val) {
   *    this.val = val;
   *    this.left = null;
   *    this.right = null;
   *    this.parent = null;
   * };
   */
  
  /**
   * @param {Node} node
   * @return {Node}
   */
  var inorderSuccessor = function (node) {
      if (node.right) {
          node = node.right;
          while (node.left) node = node.left;
          return node;
      }
      while (node.parent && node == node.parent.right) node = node.parent;
      return node.parent;
  };
  
  

• /**
   * Definition for a binary tree node.
   * class Node {
   *     val: number
   *     left: Node | null
   *     right: Node | null
   *     parent: Node | null
   *     constructor(val?: number, left?: Node | null, right?: Node | null, parent?: Node | null) {
   *         this.val = (val===undefined ? 0 : val)
   *         this.left = (left===undefined ? null : left)
   *         this.right = (right===undefined ? null : right)
   *         this.parent = (parent===undefined ? null : parent)
   *     }
   * }
   */
  
  function inorderSuccessor(node: Node | null): Node | null {
      if (node.right) {
          node = node.right;
          while (node.left) {
              node = node.left;
          }
          return node;
      }
      while (node.parent && node === node.parent.right) {
          node = node.parent;
      }
      return node.parent;
  }
  
  

All Problems

All Solutions