Welcome to Subscribe On Youtube

441. Arranging Coins

Description

You have n coins and you want to build a staircase with these coins. The staircase consists of k rows where the ith row has exactly i coins. The last row of the staircase may be incomplete.

Given the integer n, return the number of complete rows of the staircase you will build.

 

Example 1:

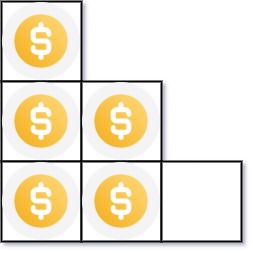
Input: n = 5
Output: 2
Explanation: Because the 3rd row is incomplete, we return 2.

Example 2:

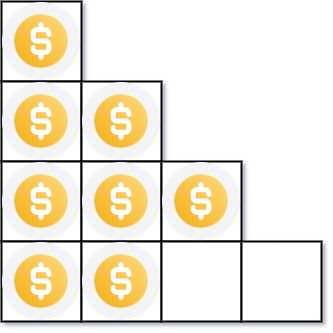
Input: n = 8
Output: 3
Explanation: Because the 4th row is incomplete, we return 3.

 

Constraints:

  • 1 <= n <= 231 - 1

Solutions

  • class Solution {
    public int arrangeCoins(int n) {
        return (int) (Math.sqrt(2) * Math.sqrt(n + 0.125) - 0.5);
    }
}

  • using LL = long;

class Solution {
public:
    int arrangeCoins(int n) {
        LL left = 1, right = n;
        while (left < right) {
            LL mid = left + right + 1 >> 1;
            LL s = (1 + mid) * mid >> 1;
            if (n < s)
                right = mid - 1;
            else
                left = mid;
        }
        return left;
    }
};

  • class Solution:
    def arrangeCoins(self, n: int) -> int:
        return int(math.sqrt(2) * math.sqrt(n + 0.125) - 0.5)


  • func arrangeCoins(n int) int {
	left, right := 1, n
	for left < right {
		mid := (left + right + 1) >> 1
		if (1+mid)*mid/2 <= n {
			left = mid
		} else {
			right = mid - 1
		}
	}
	return left
}

All Problems

All Solutions