Welcome to Subscribe On Youtube

426. Convert Binary Search Tree to Sorted Doubly Linked List

Description

Convert a Binary Search Tree to a sorted Circular Doubly-Linked List in place.

You can think of the left and right pointers as synonymous to the predecessor and successor pointers in a doubly-linked list. For a circular doubly linked list, the predecessor of the first element is the last element, and the successor of the last element is the first element.

We want to do the transformation in place. After the transformation, the left pointer of the tree node should point to its predecessor, and the right pointer should point to its successor. You should return the pointer to the smallest element of the linked list.

 

Example 1:

Input: root = [4,2,5,1,3]


Output: [1,2,3,4,5]

Explanation: The figure below shows the transformed BST. The solid line indicates the successor relationship, while the dashed line means the predecessor relationship.

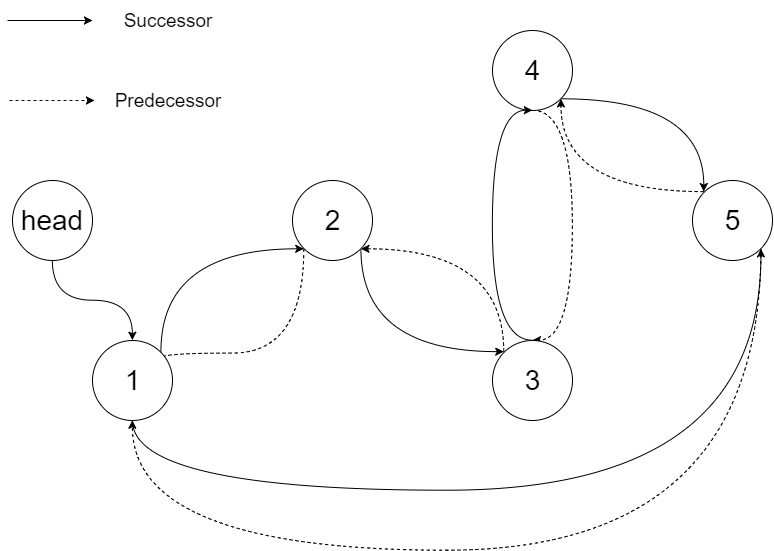
Example 2:

Input: root = [2,1,3]
Output: [1,2,3]

 

Constraints:

• The number of nodes in the tree is in the range [0, 2000].
• -1000 <= Node.val <= 1000
• All the values of the tree are unique.

Solutions

• Java
• C++
• Python
• Go
• Javascript

• /*
  // Definition for a Node.
  class Node {
      public int val;
      public Node left;
      public Node right;
  
      public Node() {}
  
      public Node(int _val) {
          val = _val;
      }
  
      public Node(int _val,Node _left,Node _right) {
          val = _val;
          left = _left;
          right = _right;
      }
  };
  */
  
  class Solution {
      private Node prev;
      private Node head;
  
      public Node treeToDoublyList(Node root) {
          if (root == null) {
              return null;
          }
          prev = null;
          head = null;
          dfs(root);
          prev.right = head;
          head.left = prev;
          return head;
      }
  
      private void dfs(Node root) {
          if (root == null) {
              return;
          }
          dfs(root.left);
          if (prev != null) {
              prev.right = root;
              root.left = prev;
          } else {
              head = root;
          }
          prev = root;
          dfs(root.right);
      }
  }
  

• /*
  // Definition for a Node.
  class Node {
  public:
      int val;
      Node* left;
      Node* right;
  
      Node() {}
  
      Node(int _val) {
          val = _val;
          left = NULL;
          right = NULL;
      }
  
      Node(int _val, Node* _left, Node* _right) {
          val = _val;
          left = _left;
          right = _right;
      }
  };
  */
  
  class Solution {
  public:
      Node* prev;
      Node* head;
  
      Node* treeToDoublyList(Node* root) {
          if (!root) return nullptr;
          prev = nullptr;
          head = nullptr;
          dfs(root);
          prev->right = head;
          head->left = prev;
          return head;
      }
  
      void dfs(Node* root) {
          if (!root) return;
          dfs(root->left);
          if (prev) {
              prev->right = root;
              root->left = prev;
          } else
              head = root;
          prev = root;
          dfs(root->right);
      }
  };
  

• """
  # Definition for a Node.
  class Node:
      def __init__(self, val, left=None, right=None):
          self.val = val
          self.left = left
          self.right = right
  """
  
  
  class Solution:
      def treeToDoublyList(self, root: 'Optional[Node]') -> 'Optional[Node]':
          def dfs(root):
              if root is None:
                  return
              nonlocal prev, head
              dfs(root.left)
              if prev:
                  prev.right = root
                  root.left = prev
              else:
                  head = root
              prev = root
              dfs(root.right)
  
          if root is None:
              return None
          head = prev = None
          dfs(root)
          prev.right = head
          head.left = prev
          return head
  
  

• /**
   * Definition for a Node.
   * type Node struct {
   *     Val int
   *     Left *Node
   *     Right *Node
   * }
   */
  
  func treeToDoublyList(root *Node) *Node {
  	if root == nil {
  		return root
  	}
  	var prev, head *Node
  
  	var dfs func(root *Node)
  	dfs = func(root *Node) {
  		if root == nil {
  			return
  		}
  		dfs(root.Left)
  		if prev != nil {
  			prev.Right = root
  			root.Left = prev
  		} else {
  			head = root
  		}
  		prev = root
  		dfs(root.Right)
  	}
  	dfs(root)
  	prev.Right = head
  	head.Left = prev
  	return head
  }
  

• /**
   * // Definition for a Node.
   * function Node(val, left, right) {
   *      this.val = val;
   *      this.left = left;
   *      this.right = right;
   *  };
   */
  
  /**
   * @param {Node} root
   * @return {Node}
   */
  var treeToDoublyList = function (root) {
      if (!root) return root;
      let prev = null;
      let head = null;
  
      function dfs(root) {
          if (!root) return;
          dfs(root.left);
          if (prev) {
              prev.right = root;
              root.left = prev;
          } else {
              head = root;
          }
          prev = root;
          dfs(root.right);
      }
      dfs(root);
      prev.right = head;
      head.left = prev;
      return head;
  };
  
  

All Problems

All Solutions