Welcome to Subscribe On Youtube
375. Guess Number Higher or Lower II
Description
We are playing the Guessing Game. The game will work as follows:
- I pick a number between
1andn. - You guess a number.
- If you guess the right number, you win the game.
- If you guess the wrong number, then I will tell you whether the number I picked is higher or lower, and you will continue guessing.
- Every time you guess a wrong number
x, you will payxdollars. If you run out of money, you lose the game.
Given a particular n, return the minimum amount of money you need to guarantee a win regardless of what number I pick.
Example 1:
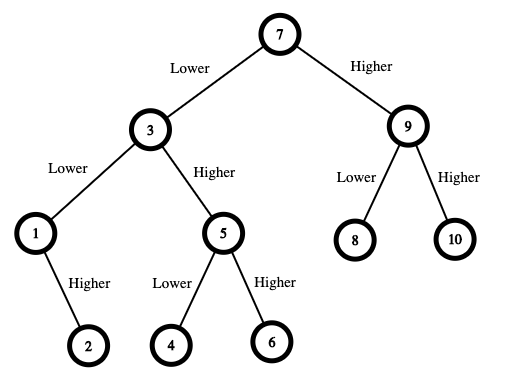
Input: n = 10 Output: 16 Explanation: The winning strategy is as follows: - The range is [1,10]. Guess 7. - If this is my number, your total is 0. Otherwise, you pay 7. - If my number is higher, the range is [8,10]. Guess 9. - If this is my number, your total is 7. Otherwise, you pay 9. - If my number is higher, it must be 10. Guess 10. Your total is 7 + 9 = 16. - If my number is lower, it must be 8. Guess 8. Your total is 7 + 9 = 16. - If my number is lower, the range is [1,6]. Guess 3. - If this is my number, your total is 7. Otherwise, you pay 3. - If my number is higher, the range is [4,6]. Guess 5. - If this is my number, your total is 7 + 3 = 10. Otherwise, you pay 5. - If my number is higher, it must be 6. Guess 6. Your total is 7 + 3 + 5 = 15. - If my number is lower, it must be 4. Guess 4. Your total is 7 + 3 + 5 = 15. - If my number is lower, the range is [1,2]. Guess 1. - If this is my number, your total is 7 + 3 = 10. Otherwise, you pay 1. - If my number is higher, it must be 2. Guess 2. Your total is 7 + 3 + 1 = 11. The worst case in all these scenarios is that you pay 16. Hence, you only need 16 to guarantee a win.
Example 2:
Input: n = 1 Output: 0 Explanation: There is only one possible number, so you can guess 1 and not have to pay anything.
Example 3:
Input: n = 2 Output: 1 Explanation: There are two possible numbers, 1 and 2. - Guess 1. - If this is my number, your total is 0. Otherwise, you pay 1. - If my number is higher, it must be 2. Guess 2. Your total is 1. The worst case is that you pay 1.
Constraints:
1 <= n <= 200
Solutions
-
class Solution { public int getMoneyAmount(int n) { int[][] dp = new int[n + 10][n + 10]; for (int l = 2; l <= n; ++l) { for (int i = 1; i + l - 1 <= n; ++i) { int j = i + l - 1; dp[i][j] = Integer.MAX_VALUE; for (int k = i; k <= j; ++k) { int t = Math.max(dp[i][k - 1], dp[k + 1][j]) + k; dp[i][j] = Math.min(dp[i][j], t); } } } return dp[1][n]; } } -
class Solution { public: int getMoneyAmount(int n) { vector<vector<int>> dp(n + 10, vector<int>(n + 10)); for (int l = 2; l <= n; ++l) { for (int i = 1; i + l - 1 <= n; ++i) { int j = i + l - 1; dp[i][j] = INT_MAX; for (int k = i; k <= j; ++k) { int t = max(dp[i][k - 1], dp[k + 1][j]) + k; dp[i][j] = min(dp[i][j], t); } } } return dp[1][n]; } }; -
class Solution: def getMoneyAmount(self, n: int) -> int: dp = [[0] * (n + 10) for _ in range(n + 10)] for l in range(2, n + 1): for i in range(1, n - l + 2): j = i + l - 1 dp[i][j] = inf for k in range(i, j + 1): t = max(dp[i][k - 1], dp[k + 1][j]) + k dp[i][j] = min(dp[i][j], t) return dp[1][n] -
func getMoneyAmount(n int) int { dp := make([][]int, n+10) for i := 0; i < len(dp); i++ { dp[i] = make([]int, n+10) } for l := 2; l <= n; l++ { for i := 1; i+l-1 <= n; i++ { j := i + l - 1 dp[i][j] = math.MaxInt32 for k := i; k <= j; k++ { t := max(dp[i][k-1], dp[k+1][j]) + k dp[i][j] = min(dp[i][j], t) } } } return dp[1][n] } -
function getMoneyAmount(n: number): number { const f: number[][] = Array.from({ length: n + 1 }, () => Array(n + 1).fill(0)); for (let i = n - 1; i; --i) { for (let j = i + 1; j <= n; ++j) { f[i][j] = j + f[i][j - 1]; for (let k = i; k < j; ++k) { f[i][j] = Math.min(f[i][j], k + Math.max(f[i][k - 1], f[k + 1][j])); } } } return f[1][n]; }