Welcome to Subscribe On Youtube
333. Largest BST Subtree
Description
Given the root of a binary tree, find the largest subtree, which is also a Binary Search Tree (BST), where the largest means subtree has the largest number of nodes.
A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties:
- The left subtree values are less than the value of their parent (root) node's value.
- The right subtree values are greater than the value of their parent (root) node's value.
Note: A subtree must include all of its descendants.
Example 1:
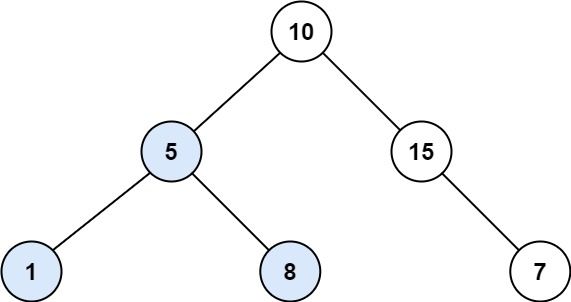
Input: root = [10,5,15,1,8,null,7] Output: 3 Explanation: The Largest BST Subtree in this case is the highlighted one. The return value is the subtree's size, which is 3.
Example 2:
Input: root = [4,2,7,2,3,5,null,2,null,null,null,null,null,1] Output: 2
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -104 <= Node.val <= 104
Follow up: Can you figure out ways to solve it with O(n) time complexity?
Solutions
The solution uses a depth-first search (DFS) strategy to explore the tree, with a use of recursion that evaluates whether each subtree meets BST criteria and calculates its size.
Core Concept
For a subtree to be considered a BST, all nodes in the left subtree must be less than the root’s value, and all nodes in the right subtree must be greater than the root’s value. Additionally, both the left and right subtrees must themselves be BSTs.
DFS Function
The dfs function is designed to return three values for each subtree it explores:
- Minimum Value (
lmi,rmi): The smallest value in the subtree. - Maximum Value (
lmx,rmx): The largest value in the subtree. - Number of Nodes (
ln,rn): The size of the largest BST within the subtree.
For a node with value None (i.e., an empty subtree), the function returns inf, -inf, and 0 to indicate that there are no values in the subtree and its size is 0.
Checking Subtree Validity
The core logic checks if the current node’s value is greater than the maximum value in the left subtree (lmx) and less than the minimum value in the right subtree (rmi). This condition ensures that the current node and its subtrees satisfy the BST property:
- If the condition holds, the current subtree rooted at
rootis a BST. The size of this subtree (ln + rn + 1) is considered for the answer (ans), which tracks the size of the largest BST found so far. - The function then returns the minimum value found in the subtree (which will be the minimum of the left subtree or the current node’s value if the left subtree is empty), the maximum value found in the subtree (which will be the maximum of the right subtree or the current node’s value), and the size of the subtree.
Handling Non-BST Subtrees
If the BST property is violated (i.e., lmx >= root.val or root.val >= rmi), the current subtree cannot be a BST. In such cases, the function returns -inf, inf, and 0 to ensure that any parent nodes will recognize this subtree as invalid for forming a BST.
Global Variable ans
The variable ans is declared as nonlocal within the dfs function, allowing it to keep track of the largest BST size found during the traversal. After exploring the entire tree, ans holds the size of the largest BST subtree.
Return Value
After calling dfs(root), the solution returns the value of ans, which by then represents the size of the largest BST contained within the original binary tree.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { private int ans; public int largestBSTSubtree(TreeNode root) { ans = 0; dfs(root); return ans; } private int[] dfs(TreeNode root) { if (root == null) { return new int[] {Integer.MAX_VALUE, Integer.MIN_VALUE, 0}; } int[] left = dfs(root.left); int[] right = dfs(root.right); if (left[1] < root.val && root.val < right[0]) { ans = Math.max(ans, left[2] + right[2] + 1); return new int[] { Math.min(root.val, left[0]), Math.max(root.val, right[1]), left[2] + right[2] + 1}; } return new int[] {Integer.MIN_VALUE, Integer.MAX_VALUE, 0}; } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int ans; int largestBSTSubtree(TreeNode* root) { ans = 0; dfs(root); return ans; } vector<int> dfs(TreeNode* root) { if (!root) return {INT_MAX, INT_MIN, 0}; auto left = dfs(root->left); auto right = dfs(root->right); if (left[1] < root->val && root->val < right[0]) { ans = max(ans, left[2] + right[2] + 1); return {min(root->val, left[0]), max(root->val, right[1]), left[2] + right[2] + 1}; } return {INT_MIN, INT_MAX, 0}; } }; -
''' >>> float("inf") inf >>> float("inf") + 1 inf >>> import math >>> float("inf") == math.inf True ''' # Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def largestBSTSubtree(self, root: Optional[TreeNode]) -> int: def dfs(root): if root is None: return inf, -inf, 0 lmi, lmx, ln = dfs(root.left) rmi, rmx, rn = dfs(root.right) nonlocal ans # this if can check if left/right is a bst # eg. if left is not bst, the returned lmi=-inf and lmx=inf, so 'lmx < root.val < rmi' is false if lmx < root.val < rmi: ans = max(ans, ln + rn + 1) # lmi is guranteed < root.val, except when left(right) is None return min(lmi, root.val), max(rmx, root.val), ln + rn + 1 return -inf, inf, 0 # if this one not bst, then all parents will not be bst ans = 0 dfs(root) return ans ############ # Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution(object): def largestBSTSubtree(self, root): """ :type root: TreeNode :rtype: int """ def helper(root): if not root: return (0, 0, float("inf"), float("-inf")) # numBST, maxNumBST, min, max lnumBST, lmaxNumBST, lmin, lmax = helper(root.left) rnumBST, rmaxNumBST, rmin, rmax = helper(root.right) numBST = -1 if lmax < root.val < rmin and lnumBST != -1 and rnumBST != -1: numBST = 1 + lnumBST + rnumBST maxNumBST = max(1, lmaxNumBST, rmaxNumBST, numBST) return numBST, maxNumBST, min(lmin, rmin, root.val), max(lmax, rmax, root.val) return helper(root)[1] -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func largestBSTSubtree(root *TreeNode) int { ans := 0 var dfs func(root *TreeNode) []int dfs = func(root *TreeNode) []int { if root == nil { return []int{math.MaxInt32, math.MinInt32, 0} } left := dfs(root.Left) right := dfs(root.Right) if left[1] < root.Val && root.Val < right[0] { ans = max(ans, left[2]+right[2]+1) return []int{min(root.Val, left[0]), max(root.Val, right[1]), left[2] + right[2] + 1} } return []int{math.MinInt32, math.MaxInt32, 0} } dfs(root) return ans }