311. Sparse Matrix Multiplication

Description

Given two sparse matrices mat1 of size m x k and mat2 of size k x n, return the result of mat1 x mat2. You may assume that multiplication is always possible.

Example 1:

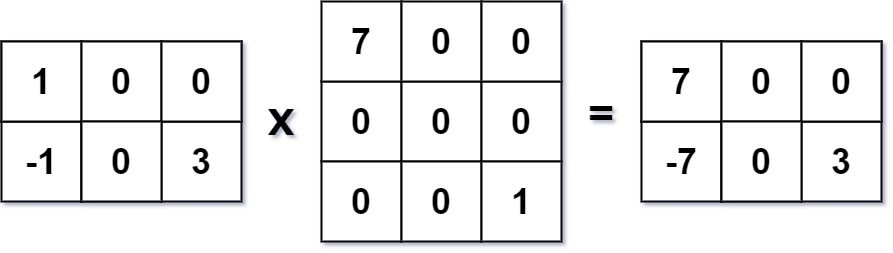
Input: mat1 = [[1,0,0],[-1,0,3]], mat2 = [[7,0,0],[0,0,0],[0,0,1]]
Output: [[7,0,0],[-7,0,3]]

Example 2:

Input: mat1 = [[0]], mat2 = [[0]]
Output: [[0]]

Constraints:

m == mat1.length
k == mat1[i].length == mat2.length
n == mat2[i].length
1 <= m, n, k <= 100
-100 <= mat1[i][j], mat2[i][j] <= 100

Solutions

Solution 1: Direct Multiplication

We can directly calculate each element in the result matrix according to the definition of matrix multiplication.

The time complexity is $O(m \times n \times k)$, and the space complexity is $O(m \times n)$. Where $m$ and $n$ are the number of rows of matrix $mat1$ and the number of columns of matrix $mat2$ respectively, and $k$ is the number of columns of matrix $mat1$ or the number of rows of matrix $mat2$.

Solution 2: Preprocessing

We can preprocess the sparse representation of the two matrices, i.e., $g1[i]$ represents the column index and value of all non-zero elements in the $i$th row of matrix $mat1$, and $g2[i]$ represents the column index and value of all non-zero elements in the $i$th row of matrix $mat2$.

Next, we traverse each row $i$, traverse each element $(k, x)$ in $g1[i]$, traverse each element $(j, y)$ in $g2[k]$, then $mat1[i][k] \times mat2[k][j]$ will correspond to $ans[i][j]$ in the result matrix, and we can accumulate all the results.

class Solution {
    public int[][] multiply(int[][] mat1, int[][] mat2) {
        int m = mat1.length, n = mat2[0].length;
        int[][] ans = new int[m][n];
        var g1 = f(mat1);
        var g2 = f(mat2);
        for (int i = 0; i < m; ++i) {
            for (int[] p : g1[i]) {
                int k = p[0], x = p[1];
                for (int[] q : g2[k]) {
                    int j = q[0], y = q[1];
                    ans[i][j] += x * y;
                }
            }
        }
        return ans;
    }

    private List<int[]>[] f(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        List<int[]>[] g = new List[m];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] != 0) {
                    g[i].add(new int[] {j, mat[i][j]});
                }
            }
        }
        return g;
    }
}

class Solution {
public:
    vector<vector<int>> multiply(vector<vector<int>>& mat1, vector<vector<int>>& mat2) {
        int m = mat1.size(), n = mat2[0].size();
        vector<vector<int>> ans(m, vector<int>(n));
        auto g1 = f(mat1), g2 = f(mat2);
        for (int i = 0; i < m; ++i) {
            for (auto& [k, x] : g1[i]) {
                for (auto& [j, y] : g2[k]) {
                    ans[i][j] += x * y;
                }
            }
        }
        return ans;
    }

    vector<vector<pair<int, int>>> f(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<pair<int, int>>> g(m);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j]) {
                    g[i].emplace_back(j, mat[i][j]);
                }
            }
        }
        return g;
    }
};

class Solution:
    def multiply(self, mat1: List[List[int]], mat2: List[List[int]]) -> List[List[int]]:
        def f(mat: List[List[int]]) -> List[List[int]]:
            g = [[] for _ in range(len(mat))]
            for i, row in enumerate(mat):
                for j, x in enumerate(row):
                    if x:
                        g[i].append((j, x))
            return g

        g1 = f(mat1)
        g2 = f(mat2)
        m, n = len(mat1), len(mat2[0])
        ans = [[0] * n for _ in range(m)]
        for i in range(m):
            for k, x in g1[i]:
                for j, y in g2[k]:
                    ans[i][j] += x * y
        return ans

func multiply(mat1 [][]int, mat2 [][]int) [][]int {
	m, n := len(mat1), len(mat2[0])
	ans := make([][]int, m)
	for i := range ans {
		ans[i] = make([]int, n)
	}
	f := func(mat [][]int) [][][2]int {
		m, n := len(mat), len(mat[0])
		g := make([][][2]int, m)
		for i := range g {
			g[i] = make([][2]int, 0, n)
			for j := range mat[i] {
				if mat[i][j] != 0 {
					g[i] = append(g[i], [2]int{j, mat[i][j]})
				}
			}
		}
		return g
	}
	g1, g2 := f(mat1), f(mat2)
	for i := range g1 {
		for _, p := range g1[i] {
			k, x := p[0], p[1]
			for _, q := range g2[k] {
				j, y := q[0], q[1]
				ans[i][j] += x * y
			}
		}
	}
	return ans
}

function multiply(mat1: number[][], mat2: number[][]): number[][] {
    const [m, n] = [mat1.length, mat2[0].length];
    const ans: number[][] = Array.from({ length: m }, () => Array.from({ length: n }, () => 0));
    const f = (mat: number[][]): number[][][] => {
        const [m, n] = [mat.length, mat[0].length];
        const ans: number[][][] = Array.from({ length: m }, () => []);
        for (let i = 0; i < m; ++i) {
            for (let j = 0; j < n; ++j) {
                if (mat[i][j] !== 0) {
                    ans[i].push([j, mat[i][j]]);
                }
            }
        }
        return ans;
    };
    const g1 = f(mat1);
    const g2 = f(mat2);
    for (let i = 0; i < m; ++i) {
        for (const [k, x] of g1[i]) {
            for (const [j, y] of g2[k]) {
                ans[i][j] += x * y;
            }
        }
    }
    return ans;
}

311 - Sparse Matrix Multiplication

311. Sparse Matrix Multiplication

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

311. Sparse Matrix Multiplication

Description

Solutions

All Problems

All Solutions