310. Minimum Height Trees

Description

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [a_i, b_i] indicates that there is an undirected edge between the two nodes a_i and b_i in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs' root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

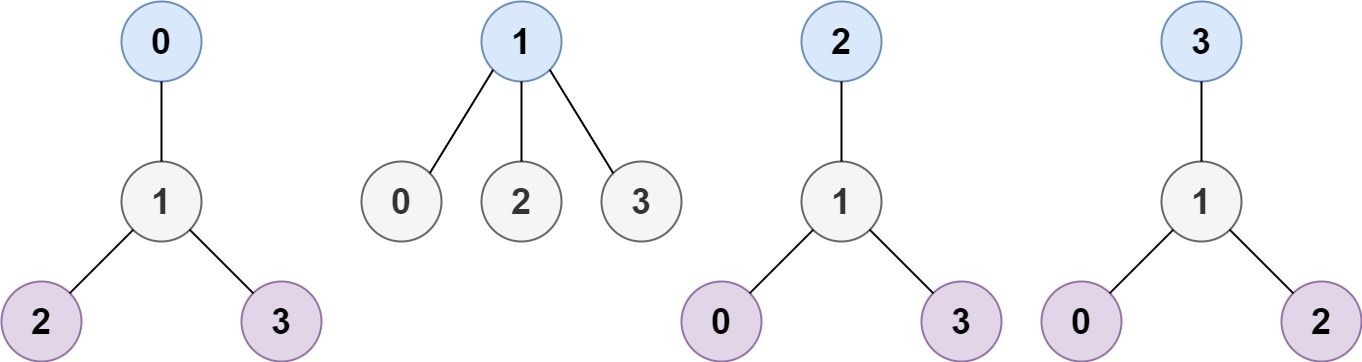
Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

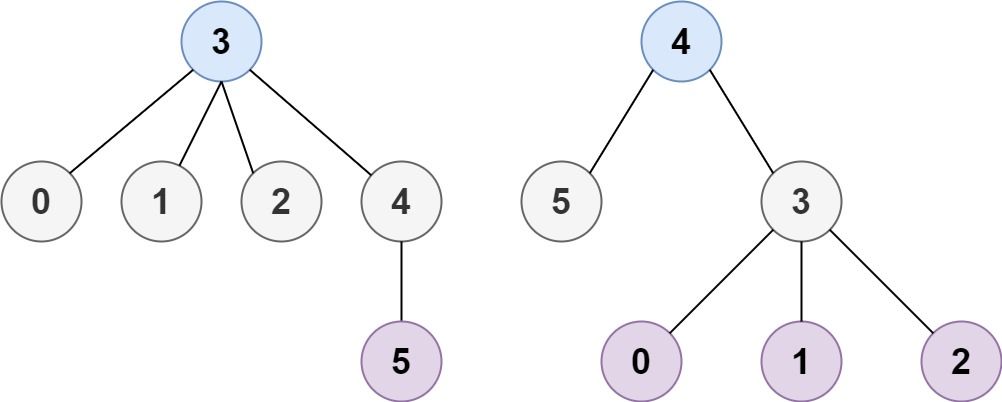
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

Constraints:

1 <= n <= 2 * 10⁴
edges.length == n - 1
0 <= a_i, b_i < n
a_i != b_i
All the pairs (a_i, b_i) are distinct.
The given input is guaranteed to be a tree and there will be no repeated edges.

Solutions

Any connected graph without simple cycles is a tree.

Start storing all nodes (leaf nodes) with only one connected edge into a queue
Then we traverse each leaf node, find the node connected to it through the graph, and delete the leaf node from the set of connected nodes
If the node becomes a leaf node after deletion, add it to the queue and delete it in the next round
Stop when the number of nodes is less than or equal to 2. At this time, the remaining one or two nodes are the root nodes of the minimum height tree we require

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        if (n == 1) {
            return Collections.singletonList(0);
        }
        List<Integer>[] g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        int[] degree = new int[n];
        for (int[] e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
            ++degree[a];
            ++degree[b];
        }
        Queue<Integer> q = new LinkedList<>();
        for (int i = 0; i < n; ++i) {
            if (degree[i] == 1) {
                q.offer(i);
            }
        }
        List<Integer> ans = new ArrayList<>();
        while (!q.isEmpty()) {
            ans.clear();
            for (int i = q.size(); i > 0; --i) {
                int a = q.poll();
                ans.add(a);
                for (int b : g[a]) {
                    if (--degree[b] == 1) {
                        q.offer(b);
                    }
                }
            }
        }
        return ans;
    }
}

class Solution {
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        if (n == 1) return {0};
        vector<vector<int>> g(n);
        vector<int> degree(n);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
            ++degree[a];
            ++degree[b];
        }
        queue<int> q;
        for (int i = 0; i < n; ++i)
            if (degree[i] == 1)
                q.push(i);
        vector<int> ans;
        while (!q.empty()) {
            ans.clear();
            for (int i = q.size(); i > 0; --i) {
                int a = q.front();
                q.pop();
                ans.push_back(a);
                for (int b : g[a])
                    if (--degree[b] == 1)
                        q.push(b);
            }
        }
        return ans;
    }
};

from typing import List, Set
from collections import defaultdict


class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        if n == 1:
            return [0]

        graph = defaultdict(set)
        for a, b in edges:
            graph[a].add(b)
            graph[b].add(a)

        # just check neighbours[] size, not indgree[] for each node
        leaves = [i for i in range(n) if len(graph[i]) == 1]

        while n > 2:
            n -= len(leaves)
            new_leaves = []
            for leaf in leaves:
                # should be only one in hashset pop(), because it's a leaf node
                neighbor = graph[leaf].pop()
                graph[neighbor].remove(leaf)
                if len(graph[neighbor]) == 1:
                    new_leaves.append(neighbor)
            leaves = new_leaves

        return leaves

###############

class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        if n == 1:
            return [0]
        g = defaultdict(list)
        degree = [0] * n
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
            degree[a] += 1 # not needed, just len(g[a]) is good enough, will update it in next round updating
            degree[b] += 1
        q = deque()
        for i in range(n):
            if degree[i] == 1:
                q.append(i)
        ans = []
        while q:
            n = len(q)
            ans.clear()
            for _ in range(n):
                a = q.popleft()
                ans.append(a)
                for b in g[a]:
                    degree[b] -= 1
                    if degree[b] == 1: # final round only 2 left (a,b), then degree[b] here will be 0, and no more node enqueue
                        q.append(b)
        return ans

func findMinHeightTrees(n int, edges [][]int) []int {
	if n == 1 {
		return []int{0}
	}
	g := make([][]int, n)
	degree := make([]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
		degree[a]++
		degree[b]++
	}
	var q []int
	for i := 0; i < n; i++ {
		if degree[i] == 1 {
			q = append(q, i)
		}
	}
	var ans []int
	for len(q) > 0 {
		ans = []int{}
		for i := len(q); i > 0; i-- {
			a := q[0]
			q = q[1:]
			ans = append(ans, a)
			for _, b := range g[a] {
				degree[b]--
				if degree[b] == 1 {
					q = append(q, b)
				}
			}
		}
	}
	return ans
}

function findMinHeightTrees(n: number, edges: number[][]): number[] {
    if (n === 1) {
        return [0];
    }
    const g: number[][] = Array.from({ length: n }, () => []);
    const degree: number[] = Array(n).fill(0);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
        ++degree[a];
        ++degree[b];
    }
    const q: number[] = [];
    for (let i = 0; i < n; ++i) {
        if (degree[i] === 1) {
            q.push(i);
        }
    }
    const ans: number[] = [];
    while (q.length > 0) {
        ans.length = 0;
        const t: number[] = [];
        for (const a of q) {
            ans.push(a);
            for (const b of g[a]) {
                if (--degree[b] === 1) {
                    t.push(b);
                }
            }
        }
        q.splice(0, q.length, ...t);
    }
    return ans;
}

310 - Minimum Height Trees

310. Minimum Height Trees

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

310. Minimum Height Trees

Description

Solutions

All Problems

All Solutions