304. Range Sum Query 2D - Immutable

Description

Given a 2D matrix matrix, handle multiple queries of the following type:

Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

You must design an algorithm where sumRegion works on O(1) time complexity.

Example 1:

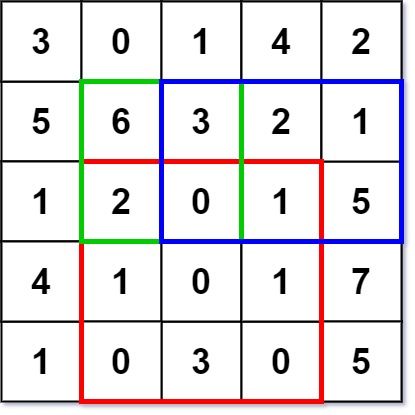
Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]

Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-10⁴ <= matrix[i][j] <= 10⁴
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
At most 10⁴ calls will be made to sumRegion.

Solutions

Solution 1: Two-dimensional Prefix Sum

We use $s[i + 1][j + 1]$ to represent the sum of all elements in the upper left part of the $i$th row and $j$th column, where indices $i$ and $j$ both start from $0$. We can get the following prefix sum formula:

\[s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + nums[i][j]\]

Then, the sum of the elements of the rectangle with $(x_1, y_1)$ and $(x_2, y_2)$ as the upper left corner and lower right corner respectively is:

\[s[x_2 + 1][y_2 + 1] - s[x_2 + 1][y_1] - s[x_1][y_2 + 1] + s[x_1][y_1]\]

In the initialization method, we preprocess the prefix sum array $s$, and in the query method, we directly return the result of the above formula.

The time complexity for initializing is $O(m \times n)$, and the time complexity for querying is $O(1)$. The space complexity is $O(m \times n)$.

class NumMatrix {
    private int[][] s;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        s = new int[m + 1][n + 1];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + matrix[i][j];
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        return s[row2 + 1][col2 + 1] - s[row2 + 1][col1] - s[row1][col2 + 1] + s[row1][col1];
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */

class NumMatrix {
public:
    vector<vector<int>> s;

    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        s.resize(m + 1, vector<int>(n + 1));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + matrix[i][j];
            }
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        return s[row2 + 1][col2 + 1] - s[row2 + 1][col1] - s[row1][col2 + 1] + s[row1][col1];
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * int param_1 = obj->sumRegion(row1,col1,row2,col2);
 */

'''
>>> a = [ [1,2,3], [4,5,6] ]
>>> b = a.copy()
>>> b
[[1, 2, 3], [4, 5, 6]]
'''
class NumMatrix:
    def __init__(self, matrix: List[List[int]]):
        m, n = len(matrix), len(matrix[0])
        self.s = [[0] * (n + 1) for _ in range(m + 1)]
        for i, row in enumerate(matrix):
            for j, v in enumerate(row):
                self.s[i + 1][j + 1] = (
                    self.s[i][j + 1] + self.s[i + 1][j] - self.s[i][j] + v
                )

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return (
            self.s[row2 + 1][col2 + 1]
            - self.s[row2 + 1][col1]
            - self.s[row1][col2 + 1]
            + self.s[row1][col1]
        )


# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)

############

class NumMatrix(object):
  def __init__(self, matrix):
    """
    initialize your data structure here.
    :type matrix: List[List[int]]
    """
    self.dp = [[0] * len(matrix[0]) for i in range(0, len(matrix))]
    for i in range(0, len(matrix)):
      for j in range(0, len(matrix[0])):
        if i == 0:
          self.dp[0][j] = self.dp[0][j - 1] + matrix[i][j]
        elif j == 0:
          self.dp[i][0] = self.dp[i - 1][0] + matrix[i][j]
        else:
          self.dp[i][j] = self.dp[i - 1][j] + self.dp[i][j - 1] - self.dp[i - 1][j - 1] + matrix[i][j]

  def sumRegion(self, row1, col1, row2, col2):
    """
    sum of elements matrix[(row1,col1)..(row2,col2)], inclusive.
    :type row1: int
    :type col1: int
    :type row2: int
    :type col2: int
    :rtype: int
    """
    dp = self.dp

    diagSum = dp[row1 - 1][col1 - 1]
    totalSum = dp[row2][col2]
    leftSum = dp[row2][col1 - 1]
    upSum = dp[row1 - 1][col2]
    if row1 == 0:
      upSum = 0
      diagSum = 0
    if col1 == 0:
      leftSum = 0
      diagSum = 0
    return totalSum - leftSum - upSum + diagSum

type NumMatrix struct {
	s [][]int
}

func Constructor(matrix [][]int) NumMatrix {
	m, n := len(matrix), len(matrix[0])
	s := make([][]int, m+1)
	for i := range s {
		s[i] = make([]int, n+1)
	}
	for i, row := range matrix {
		for j, v := range row {
			s[i+1][j+1] = s[i+1][j] + s[i][j+1] - s[i][j] + v
		}
	}
	return NumMatrix{s}
}

func (this *NumMatrix) SumRegion(row1 int, col1 int, row2 int, col2 int) int {
	return this.s[row2+1][col2+1] - this.s[row2+1][col1] - this.s[row1][col2+1] + this.s[row1][col1]
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * obj := Constructor(matrix);
 * param_1 := obj.SumRegion(row1,col1,row2,col2);
 */

class NumMatrix {
    private s: number[][];

    constructor(matrix: number[][]) {
        const m = matrix.length;
        const n = matrix[0].length;
        this.s = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
        for (let i = 0; i < m; ++i) {
            for (let j = 0; j < n; ++j) {
                this.s[i + 1][j + 1] =
                    this.s[i + 1][j] + this.s[i][j + 1] - this.s[i][j] + matrix[i][j];
            }
        }
    }

    sumRegion(row1: number, col1: number, row2: number, col2: number): number {
        return (
            this.s[row2 + 1][col2 + 1] -
            this.s[row2 + 1][col1] -
            this.s[row1][col2 + 1] +
            this.s[row1][col1]
        );
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * var obj = new NumMatrix(matrix)
 * var param_1 = obj.sumRegion(row1,col1,row2,col2)
 */

/**
 * @param {number[][]} matrix
 */
var NumMatrix = function (matrix) {
    const m = matrix.length;
    const n = matrix[0].length;
    this.s = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            this.s[i + 1][j + 1] =
                this.s[i + 1][j] + this.s[i][j + 1] - this.s[i][j] + matrix[i][j];
        }
    }
};

/**
 * @param {number} row1
 * @param {number} col1
 * @param {number} row2
 * @param {number} col2
 * @return {number}
 */
NumMatrix.prototype.sumRegion = function (row1, col1, row2, col2) {
    return (
        this.s[row2 + 1][col2 + 1] -
        this.s[row2 + 1][col1] -
        this.s[row1][col2 + 1] +
        this.s[row1][col1]
    );
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * var obj = new NumMatrix(matrix)
 * var param_1 = obj.sumRegion(row1,col1,row2,col2)
 */

/**
 * Your NumMatrix object will be instantiated and called as such:
 * let obj = NumMatrix::new(matrix);
 * let ret_1: i32 = obj.sum_region(row1, col1, row2, col2);
 */

struct NumMatrix {
    // Of size (N + 1) * (M + 1)
    prefix_vec: Vec<Vec<i32>>,
    n: usize,
    m: usize,
    is_initialized: bool,
    ref_vec: Vec<Vec<i32>>,
}

/**
 * `&self` means the method takes an immutable reference.
 * If you need a mutable reference, change it to `&mut self` instead.
 */
impl NumMatrix {
    fn new(matrix: Vec<Vec<i32>>) -> Self {
        NumMatrix {
            prefix_vec: vec![vec![0; matrix[0].len() + 1]; matrix.len() + 1],
            n: matrix.len(),
            m: matrix[0].len(),
            is_initialized: false,
            ref_vec: matrix,
        }
    }

    fn sum_region(&mut self, row1: i32, col1: i32, row2: i32, col2: i32) -> i32 {
        if !self.is_initialized {
            self.initialize_prefix_vec();
        }
        // Since i32 will let `rustc` complain, just make it happy
        let row1: usize = row1 as usize;
        let col1: usize = col1 as usize;
        let row2: usize = row2 as usize;
        let col2: usize = col2 as usize;
        // Return the value in O(1)
        self.prefix_vec[row2 + 1][col2 + 1] -
            self.prefix_vec[row2 + 1][col1] -
            self.prefix_vec[row1][col2 + 1] +
            self.prefix_vec[row1][col1]
    }

    fn initialize_prefix_vec(&mut self) {
        // Initialize the prefix sum vector
        for i in 0..self.n {
            for j in 0..self.m {
                self.prefix_vec[i + 1][j + 1] =
                    self.prefix_vec[i][j + 1] +
                    self.prefix_vec[i + 1][j] -
                    self.prefix_vec[i][j] +
                    self.ref_vec[i][j];
            }
        }
        self.is_initialized = true;
    }
}

304 - Range Sum Query 2D - Immutable

304. Range Sum Query 2D - Immutable

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

304. Range Sum Query 2D - Immutable

Description

Solutions

All Problems

All Solutions