298. Binary Tree Longest Consecutive Sequence

Description

Given the root of a binary tree, return the length of the longest consecutive sequence path.

A consecutive sequence path is a path where the values increase by one along the path.

Note that the path can start at any node in the tree, and you cannot go from a node to its parent in the path.

Example 1:

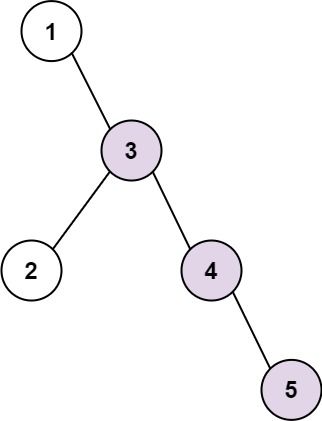
Input: root = [1,null,3,2,4,null,null,null,5]
Output: 3
Explanation: Longest consecutive sequence path is 3-4-5, so return 3.

Example 2:

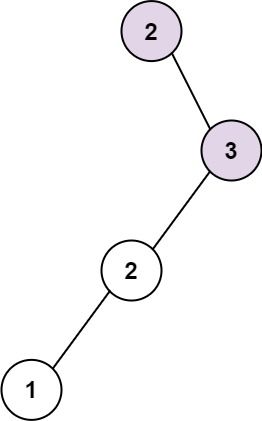
Input: root = [2,null,3,2,null,1]
Output: 2
Explanation: Longest consecutive sequence path is 2-3, not 3-2-1, so return 2.

Constraints:

The number of nodes in the tree is in the range [1, 3 * 10⁴].
-3 * 10⁴ <= Node.val <= 3 * 10⁴

Solutions

DFS or BFS.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int ans;

    public int longestConsecutive(TreeNode root) {
        dfs(root);
        return ans;
    }

    private int dfs(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int l = dfs(root.left) + 1;
        int r = dfs(root.right) + 1;
        if (root.left != null && root.left.val - root.val != 1) {
            l = 1;
        }
        if (root.right != null && root.right.val - root.val != 1) {
            r = 1;
        }
        int t = Math.max(l, r);
        ans = Math.max(ans, t);
        return t;
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int longestConsecutive(TreeNode* root) {
        int ans = 0;
        function<int(TreeNode*)> dfs = [&](TreeNode* root) {
            if (!root) {
                return 0;
            }
            int l = dfs(root->left) + 1;
            int r = dfs(root->right) + 1;
            if (root->left && root->left->val - root->val != 1) {
                l = 1;
            }
            if (root->right && root->right->val - root->val != 1) {
                r = 1;
            }
            int t = max(l, r);
            ans = max(ans, t);
            return t;
        };
        dfs(root);
        return ans;
    }
};

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

# dfs
class Solution:
    def longestConsecutive(self, root: TreeNode) -> int:
        maxLen = 0

        # curLen: consecutive length until parent node
        def dfs(root: TreeNode, lastVal: int, curLen: int) -> None:
            nonlocal maxLen
            if not root:
                return

            curLen = (curLen + 1) if (not lastVal) and root.val == lastVal + 1 else 1
            maxLen = max(maxLen, curLen)

            dfs(root.left, root.val, curLen)
            dfs(root.right, root.val, curLen)

        dfs(root, None, 0)
        return maxLen

############

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

from collections import deque

# iterative, bfs
class Solution:
    def longestConsecutive(self, root: TreeNode) -> int:
        if not root:
            return 0
        
        max_length = 0
        # Queue elements are tuples: (current node, length of consecutive sequence)
        queue = deque([(root, 1)])
        
        while queue:
            current, length = queue.popleft()
            max_length = max(max_length, length)
            
            for neighbor in [current.left, current.right]:
                if neighbor:
                    # Check if neighbor is consecutive
                    if neighbor.val == current.val + 1:
                        queue.append((neighbor, length + 1))
                    else:
                        queue.append((neighbor, 1))
        
        return max_length

############

class Solution:
    def longestConsecutive(self, root: Optional[TreeNode]) -> int:
        def dfs(root: Optional[TreeNode]) -> int:
            if root is None:
                return 0
            l = dfs(root.left) + 1
            r = dfs(root.right) + 1
            if root.left and root.left.val - root.val != 1:
                l = 1
            if root.right and root.right.val - root.val != 1:
                r = 1
            t = max(l, r)
            nonlocal ans
            ans = max(ans, t)
            return t

        ans = 0
        dfs(root)
        return ans

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func longestConsecutive(root *TreeNode) (ans int) {
	var dfs func(*TreeNode) int
	dfs = func(root *TreeNode) int {
		if root == nil {
			return 0
		}
		l := dfs(root.Left) + 1
		r := dfs(root.Right) + 1
		if root.Left != nil && root.Left.Val-root.Val != 1 {
			l = 1
		}
		if root.Right != nil && root.Right.Val-root.Val != 1 {
			r = 1
		}
		t := max(l, r)
		ans = max(ans, t)
		return t
	}
	dfs(root)
	return
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function longestConsecutive(root: TreeNode | null): number {
    let ans = 0;
    const dfs = (root: TreeNode | null): number => {
        if (root === null) {
            return 0;
        }
        let l = dfs(root.left) + 1;
        let r = dfs(root.right) + 1;
        if (root.left && root.left.val - root.val !== 1) {
            l = 1;
        }
        if (root.right && root.right.val - root.val !== 1) {
            r = 1;
        }
        const t = Math.max(l, r);
        ans = Math.max(ans, t);
        return t;
    };
    dfs(root);
    return ans;
}

298 - Binary Tree Longest Consecutive Sequence

298. Binary Tree Longest Consecutive Sequence

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

298. Binary Tree Longest Consecutive Sequence

Description

Solutions

All Problems

All Solutions