Welcome to Subscribe On Youtube

277. Find the Celebrity

Description

Suppose you are at a party with n people labeled from 0 to n - 1 and among them, there may exist one celebrity. The definition of a celebrity is that all the other n - 1 people know the celebrity, but the celebrity does not know any of them.

Now you want to find out who the celebrity is or verify that there is not one. You are only allowed to ask questions like: "Hi, A. Do you know B?" to get information about whether A knows B. You need to find out the celebrity (or verify there is not one) by asking as few questions as possible (in the asymptotic sense).

You are given a helper function bool knows(a, b) that tells you whether a knows b. Implement a function int findCelebrity(n). There will be exactly one celebrity if they are at the party.

Return the celebrity's label if there is a celebrity at the party. If there is no celebrity, return -1.

 

Example 1:

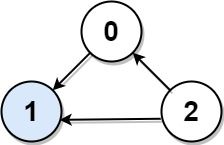
Input: graph = [[1,1,0],[0,1,0],[1,1,1]]
Output: 1
Explanation: There are three persons labeled with 0, 1 and 2. graph[i][j] = 1 means person i knows person j, otherwise graph[i][j] = 0 means person i does not know person j. The celebrity is the person labeled as 1 because both 0 and 2 know him but 1 does not know anybody.

Example 2:

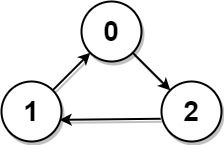
Input: graph = [[1,0,1],[1,1,0],[0,1,1]]
Output: -1
Explanation: There is no celebrity.

 

Constraints:

• n == graph.length == graph[i].length
• 2 <= n <= 100
• graph[i][j] is 0 or 1.
• graph[i][i] == 1

 

Follow up: If the maximum number of allowed calls to the API knows is 3 * n, could you find a solution without exceeding the maximum number of calls?

Solutions

Set the candidate res to 0. The principle is to traverse once. For the traversed person i, if the candidate res knows i, set the candidate res to i. After completing the traversal, check whether the candidate res is really a celebrity, if it is found not to be a celebrity, return -1, if there is no conflict, return res.

Follow up - reduce api calls

It can also further reduce the amount of API calls. The method of finding candidates is the same as above, but it is divided into two sections when verifying.

• First verify everyone in front of the candidate. If the candidate knows anyone, or anyone does not know the candidate, return -1 directly.
• Then verify the people behind the candidate. At this time, you only need to verify whether anyone does not know the candidate.
• Because we have ensured that the candidate will not know anyone before candidate

• Java
• C++
• Python
• Go

• /* The knows API is defined in the parent class Relation.
        boolean knows(int a, int b); */
  
  public class Solution extends Relation {
      public int findCelebrity(int n) {
          int ans = 0;
          for (int i = 1; i < n; ++i) {
              if (knows(ans, i)) {
                  ans = i;
              }
          }
          for (int i = 0; i < n; ++i) {
              if (ans != i) {
                  if (knows(ans, i) || !knows(i, ans)) {
                      return -1;
                  }
              }
          }
          return ans;
      }
  }
  

• /* The knows API is defined for you.
        bool knows(int a, int b); */
  
  class Solution {
  public:
      int findCelebrity(int n) {
          int ans = 0;
          for (int i = 1; i < n; ++i) {
              if (knows(ans, i)) {
                  ans = i;
              }
          }
          for (int i = 0; i < n; ++i) {
              if (ans != i) {
                  if (knows(ans, i) || !knows(i, ans)) {
                      return -1;
                  }
              }
          }
          return ans;
      }
  };
  

• # The knows API is already defined for you.
  # return a bool, whether a knows b
  # def knows(a: int, b: int) -> bool:
  
  
  class Solution:
      def findCelebrity(self, n: int) -> int:
          ans = 0
          for i in range(1, n):
              if knows(ans, i):
                  ans = i
          for i in range(n):
              if ans != i:
                  if knows(ans, i) or not knows(i, ans):
                      return -1
          return ans
  
  

• /**
   * The knows API is already defined for you.
   *     knows := func(a int, b int) bool
   */
  func solution(knows func(a int, b int) bool) func(n int) int {
  	return func(n int) int {
  		ans := 0
  		for i := 1; i < n; i++ {
  			if knows(ans, i) {
  				ans = i
  			}
  		}
  		for i := 0; i < n; i++ {
  			if ans != i {
  				if knows(ans, i) || !knows(i, ans) {
  					return -1
  				}
  			}
  		}
  		return ans
  	}
  }
  

All Problems

All Solutions