Question

Formatted question description: https://leetcode.ca/all/276.html

You are painting a fence of n posts with k different colors. You must paint the posts following these rules:

Every post must be painted exactly one color.
There cannot be three or more consecutive posts with the same color.

Given the two integers n and k, return the number of ways you can paint the fence.

Example 1:

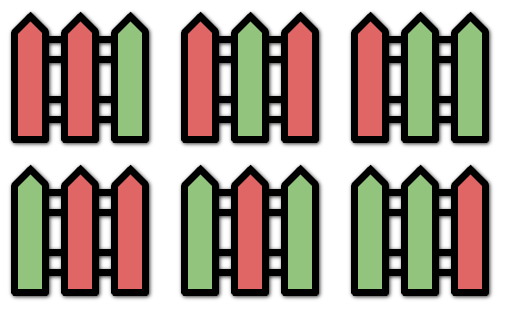
Input: n = 3, k = 2
Output: 6
Explanation: All the possibilities are shown.
Note that painting all the posts red or all the posts green is invalid because there cannot be three posts in a row with the same color.

Example 2:

Input: n = 1, k = 1
Output: 1

Example 3:

Input: n = 7, k = 2
Output: 42

Constraints:

1 <= n <= 50
1 <= k <= 10⁵
The testcases are generated such that the answer is in the range [0, 2³¹ - 1] for the given n and k.

Algorithm

If n == 0 or k == 0, painting the fence as required is not feasible, therefore the function should return 0.

This solution employs dynamic programming. It involves initializing a 2D array dp with n rows and 2 columns. In this array:

dp[i][1] indicates the count of possible ways to paint the first i + 1 fence posts, with the i-th post painted the same color as the one before it.
Conversely, dp[i][0] signifies the number of ways to paint the first i + 1 fence posts, with the i-th post painted a different color from its predecessor.

Initially, set dp[0][0] = 0 and dp[0][1] = k, reflecting the scenario with just one post. For i > 0:

dp[i][0] = dp[i - 1][1] because for the i-th post to match the color of its predecessor, it must adopt the configuration of the previous post having a unique color.
dp[i][1] = (dp[i - 1][0] + dp[i - 1][1]) * (k - 1) because to paint the i-th post a different color from the i-1-th post, you have k - 1 color options available. This calculation sums the possible configurations from the previous post and multiplies by the color options excluding the color used previously.

To obtain the total configurations for painting the fence, sum the last row values of dp: dp[n - 1][0] + dp[n - 1][1], which gives the final answer.

Code

public class Paint_Fence {

    public static void main(String[] args) {
        Paint_Fence out = new Paint_Fence();

        Solution s1 = out.new Solution();
        Solution_noArray s2 = out.new Solution_noArray();

        System.out.println(s1.numWays(3, 2)); // 6
        System.out.println(s2.numWays(3, 2));
    }

    class Solution {
        public int numWays(int n, int k) {
            if (n == 0 || k == 0)
                return 0;

            // `dp[i][0]` same color
            // `dp[i][1]` different color
            int[][] dp = new int[n][2];
            dp[0][0] = 0;
            dp[0][1] = k;
            for (int i = 1; i < n; i++) {
                dp[i][0] = dp[i - 1][1]; // or else 3-posts the same color
                dp[i][1] = (dp[i - 1][0] + dp[i - 1][1]) * (k - 1);
            }
            return dp[n - 1][0] + dp[n - 1][1];
        }
    }

    public class Solution_noArray {
        public int numWays(int n, int k) {
            if (n == 0) return 0;
            int same = 0, diff = k;
            for (int i = 2; i <= n; ++i) {
                int t = diff;
                diff = (same + diff) * (k - 1);
                same = t;
            }
            return same + diff;
        }
    }
}

############

class Solution {
    public int numWays(int n, int k) {
        int[][] dp = new int[n][2];
        dp[0][0] = k;
        for (int i = 1; i < n; ++i) {
            dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) * (k - 1);
            dp[i][1] = dp[i - 1][0];
        }
        return dp[n - 1][0] + dp[n - 1][1];
    }
}

// OJ: https://leetcode.com/problems/paint-fence/
// Time: O(N)
// Space: O(1)
class Solution {
public:
    int numWays(int n, int k) {
        if (k == 1 && n >= 3) return 0;
        int dp[2] = {k, 0};
        for (int i = 1; i < n; ++i) {
            int next[2] = {(k - 1) * (dp[0] + dp[1]), dp[0]};
            swap(next, dp);
        }
        return dp[0] + dp[1];
    }
};

class Solution:
    def numWays(self, n: int, k: int) -> int:
        # `dp[i][0]` same color
        # `dp[i][1]` different color
        dp = [[0] * 2 for _ in range(n)]
        dp[0][1] = k
        for i in range(1, n):
            dp[i][0] = dp[i - 1][1] # same as previous, or else 3-posts the same color
            dp[i][1] = (dp[i - 1][0] + dp[i - 1][1]) * (k - 1) # not the same as previous
        return sum(dp[-1])

############

class Solution(object):
  def numWays(self, n, k):
    """
    :type n: int
    :type k: int
    :rtype: int
    """
    if n > 2 and k == 1:
      return 0
    if n < 2:
      return n * k
    pre = k * k
    ppre = k
    for i in range(2, n):
      tmp = pre
      pre = (k - 1) * (pre + ppre)
      ppre = tmp
    return pre

func numWays(n int, k int) int {
	dp := make([][]int, n)
	for i := range dp {
		dp[i] = make([]int, 2)
	}
	dp[0][0] = k
	for i := 1; i < n; i++ {
		dp[i][0] = (dp[i-1][0] + dp[i-1][1]) * (k - 1)
		dp[i][1] = dp[i-1][0]
	}
	return dp[n-1][0] + dp[n-1][1]
}

function numWays(n: number, k: number): number {
    const f: number[] = Array(n).fill(0);
    const g: number[] = Array(n).fill(0);
    f[0] = k;
    for (let i = 1; i < n; ++i) {
        f[i] = (f[i - 1] + g[i - 1]) * (k - 1);
        g[i] = f[i - 1];
    }
    return f[n - 1] + g[n - 1];
}

276 - Paint Fence

Question

Algorithm

Code

All Problems

All Solutions

Welcome to Subscribe On Youtube

Question

Algorithm

Code

All Problems

All Solutions