Welcome to Subscribe On Youtube

261. Graph Valid Tree

Description

You have a graph of n nodes labeled from 0 to n - 1. You are given an integer n and a list of edges where edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the graph.

Return true if the edges of the given graph make up a valid tree, and false otherwise.

 

Example 1:

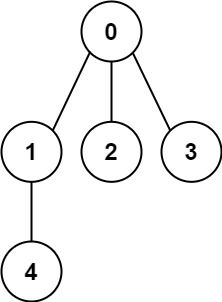
Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true

Example 2:

Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false

 

Constraints:

• 1 <= n <= 2000
• 0 <= edges.length <= 5000
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• There are no self-loops or repeated edges.

Solutions

Union find.

• Java
• C++
• Python
• Go
• Javascript

• class Solution {
      private int[] p;
  
      public boolean validTree(int n, int[][] edges) {
          p = new int[n];
          for (int i = 0; i < n; ++i) {
              p[i] = i;
          }
          for (int[] e : edges) {
              int a = e[0], b = e[1];
              if (find(a) == find(b)) {
                  return false;
              }
              p[find(a)] = find(b);
              --n;
          }
          return n == 1;
      }
  
      private int find(int x) {
          if (p[x] != x) {
              p[x] = find(p[x]);
          }
          return p[x];
      }
  }
  

• class Solution {
  public:
      vector<int> p;
  
      bool validTree(int n, vector<vector<int>>& edges) {
          p.resize(n);
          for (int i = 0; i < n; ++i) p[i] = i;
          for (auto& e : edges) {
              int a = e[0], b = e[1];
              if (find(a) == find(b)) return 0;
              p[find(a)] = find(b);
              --n;
          }
          return n == 1;
      }
  
      int find(int x) {
          if (p[x] != x) p[x] = find(p[x]);
          return p[x];
      }
  };
  

• class Solution:
      def validTree(self, n: int, edges: List[List[int]]) -> bool:
          def find(x):
              if p[x] != x:
                  p[x] = find(p[x])
              return p[x]
  
          p = list(range(n))
          for a, b in edges:
              if find(a) == find(b):
                  return False
              p[find(a)] = find(b)
              n -= 1
          return n == 1
  
  

• func validTree(n int, edges [][]int) bool {
  	p := make([]int, n)
  	for i := range p {
  		p[i] = i
  	}
  	var find func(x int) int
  	find = func(x int) int {
  		if p[x] != x {
  			p[x] = find(p[x])
  		}
  		return p[x]
  	}
  	for _, e := range edges {
  		a, b := e[0], e[1]
  		if find(a) == find(b) {
  			return false
  		}
  		p[find(a)] = find(b)
  		n--
  	}
  	return n == 1
  }
  

• /**
   * @param {number} n
   * @param {number[][]} edges
   * @return {boolean}
   */
  var validTree = function (n, edges) {
      let p = new Array(n);
      for (let i = 0; i < n; ++i) {
          p[i] = i;
      }
      function find(x) {
          if (p[x] != x) {
              p[x] = find(p[x]);
          }
          return p[x];
      }
      for (const [a, b] of edges) {
          if (find(a) == find(b)) {
              return false;
          }
          p[find(a)] = find(b);
          --n;
      }
      return n == 1;
  };
  
  

All Problems

All Solutions