Welcome to Subscribe On Youtube

223. Rectangle Area

Description

Given the coordinates of two rectilinear rectangles in a 2D plane, return the total area covered by the two rectangles.

The first rectangle is defined by its bottom-left corner (ax1, ay1) and its top-right corner (ax2, ay2).

The second rectangle is defined by its bottom-left corner (bx1, by1) and its top-right corner (bx2, by2).

 

Example 1:

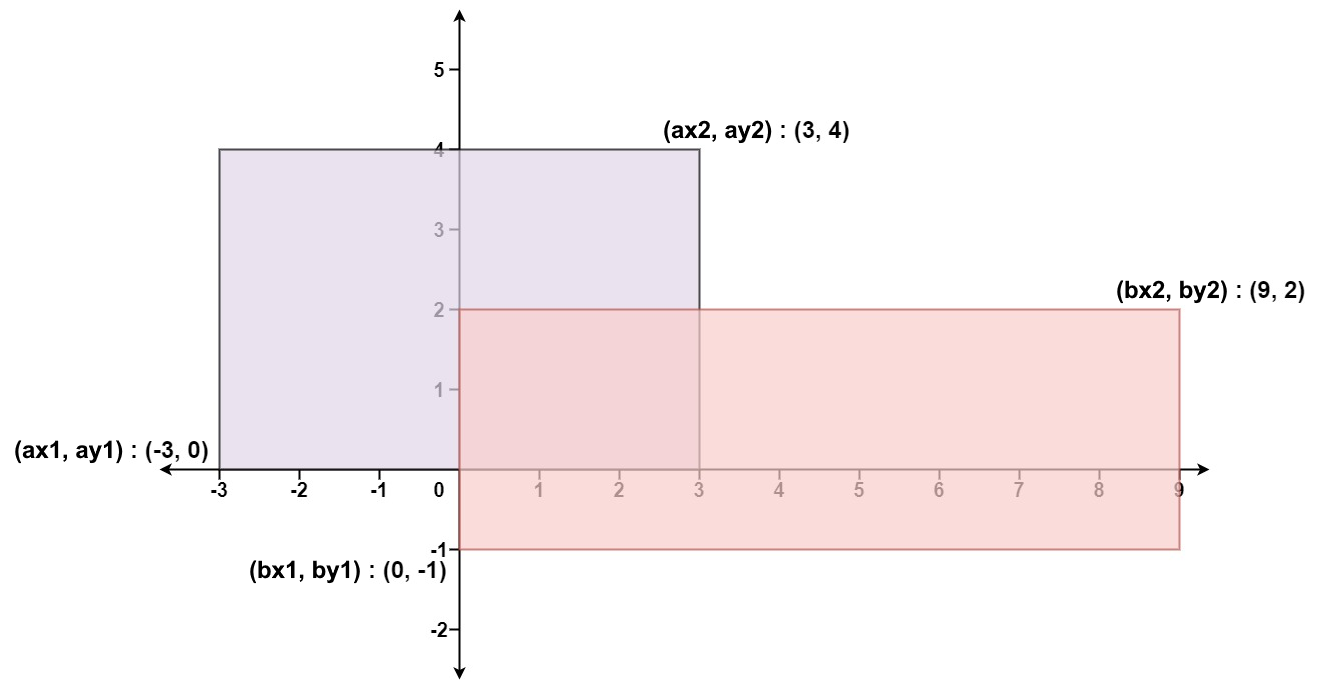
Input: ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
Output: 45

Example 2:

Input: ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
Output: 16

 

Constraints:

• -104 <= ax1 <= ax2 <= 104
• -104 <= ay1 <= ay2 <= 104
• -104 <= bx1 <= bx2 <= 104
• -104 <= by1 <= by2 <= 104

Solutions

Solution 1: Calculate Overlapping Area

First, we calculate the area of the two rectangles separately, denoted as $a$ and $b$. Then we calculate the overlapping width $width$ and height $height$. The overlapping area is $max(width, 0) \times max(height, 0)$. Finally, we subtract the overlapping area from $a$ and $b$.

The time complexity is $O(1)$, and the space complexity is $O(1)$.

• Java
• C++
• Python
• Go
• TypeScript
• C#

• class Solution {
      public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
          int a = (ax2 - ax1) * (ay2 - ay1);
          int b = (bx2 - bx1) * (by2 - by1);
          int width = Math.min(ax2, bx2) - Math.max(ax1, bx1);
          int height = Math.min(ay2, by2) - Math.max(ay1, by1);
          return a + b - Math.max(height, 0) * Math.max(width, 0);
      }
  }
  
  

• class Solution {
  public:
      int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
          int a = (ax2 - ax1) * (ay2 - ay1);
          int b = (bx2 - bx1) * (by2 - by1);
          int width = min(ax2, bx2) - max(ax1, bx1);
          int height = min(ay2, by2) - max(ay1, by1);
          return a + b - max(height, 0) * max(width, 0);
      }
  };
  

• class Solution:
      def computeArea(
          self,
          ax1: int,
          ay1: int,
          ax2: int,
          ay2: int,
          bx1: int,
          by1: int,
          bx2: int,
          by2: int,
      ) -> int:
          a = (ax2 - ax1) * (ay2 - ay1)
          b = (bx2 - bx1) * (by2 - by1)
          width = min(ax2, bx2) - max(ax1, bx1)
          height = min(ay2, by2) - max(ay1, by1)
          return a + b - max(height, 0) * max(width, 0)
  
  ############
  
  class Solution(object):
    def computeArea(self, A, B, C, D, E, F, G, H):
      """
      :type A: int
      :type B: int
      :type C: int
      :type D: int
      :type E: int
      :type F: int
      :type G: int
      :type H: int
      :rtype: int
      """
      area = (C - A) * (D - B) + (G - E) * (H - F)
      overlap = max(min(C, G) - max(A, E), 0) * max(min(D, H) - max(B, F), 0)
      return area - overlap
  
  
  

• func computeArea(ax1 int, ay1 int, ax2 int, ay2 int, bx1 int, by1 int, bx2 int, by2 int) int {
  	a := (ax2 - ax1) * (ay2 - ay1)
  	b := (bx2 - bx1) * (by2 - by1)
  	width := min(ax2, bx2) - max(ax1, bx1)
  	height := min(ay2, by2) - max(ay1, by1)
  	return a + b - max(height, 0)*max(width, 0)
  }
  

• function computeArea(
      ax1: number,
      ay1: number,
      ax2: number,
      ay2: number,
      bx1: number,
      by1: number,
      bx2: number,
      by2: number,
  ): number {
      const a = (ax2 - ax1) * (ay2 - ay1);
      const b = (bx2 - bx1) * (by2 - by1);
      const width = Math.min(ax2, bx2) - Math.max(ax1, bx1);
      const height = Math.min(ay2, by2) - Math.max(ay1, by1);
      return a + b - Math.max(width, 0) * Math.max(height, 0);
  }
  
  

• public class Solution {
      public int ComputeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
          int a = (ax2 - ax1) * (ay2 - ay1);
          int b = (bx2 - bx1) * (by2 - by1);
          int width = Math.Min(ax2, bx2) - Math.Max(ax1, bx1);
          int height = Math.Min(ay2, by2) - Math.Max(ay1, by1);
          return a + b - Math.Max(height, 0) * Math.Max(width, 0);
      }
  }
  

All Problems

All Solutions