Welcome to Subscribe On Youtube
222. Count Complete Tree Nodes
Description
Given the root of a complete binary tree, return the number of the nodes in the tree.
According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
Design an algorithm that runs in less than O(n) time complexity.
Example 1:
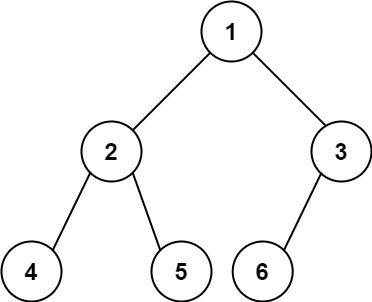
Input: root = [1,2,3,4,5,6] Output: 6
Example 2:
Input: root = [] Output: 0
Example 3:
Input: root = [1] Output: 1
Constraints:
- The number of nodes in the tree is in the range
[0, 5 * 104]. 0 <= Node.val <= 5 * 104- The tree is guaranteed to be complete.
Solutions
Solution 1: Recursion
We recursively traverse the entire tree and count the number of nodes.
The time complexity is $O(n)$, and the space complexity is $O(n)$, where $n$ is the number of nodes in the tree.
Solution 2: Binary Search
For this problem, we can also take advantage of the characteristics of a complete binary tree to design a faster algorithm.
Characteristics of a complete binary tree: leaf nodes can only appear on the bottom and second-to-bottom layers, and the leaf nodes on the bottom layer are concentrated on the left side of the tree. It should be noted that a full binary tree is definitely a complete binary tree, but a complete binary tree is not necessarily a full binary tree.
If the number of layers in a full binary tree is $h$, then the total number of nodes is $2^h - 1$.
We first count the heights of the left and right subtrees of $root$, denoted as $left$ and $right$.
- If $left = right$, it means that the left subtree is a full binary tree, so the total number of nodes in the left subtree is $2^{left} - 1$. Plus the $root$ node, it is $2^{left}$. Then we recursively count the right subtree.
- If $left > right$, it means that the right subtree is a full binary tree, so the total number of nodes in the right subtree is $2^{right} - 1$. Plus the $root$ node, it is $2^{right}$. Then we recursively count the left subtree.
The time complexity is $O(\log^2 n)$. (square of tree-height)
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public int countNodes(TreeNode root) { if (root == null) { return 0; } int left = depth(root.left); int right = depth(root.right); if (left == right) { return (1 << left) + countNodes(root.right); } return (1 << right) + countNodes(root.left); } private int depth(TreeNode root) { int d = 0; for (; root != null; root = root.left) { ++d; } return d; } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int countNodes(TreeNode* root) { if (!root) { return 0; } int left = depth(root->left); int right = depth(root->right); if (left == right) { return (1 << left) + countNodes(root->right); } return (1 << right) + countNodes(root->left); } int depth(TreeNode* root) { int d = 0; for (; root; root = root->left) { ++d; } return d; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def countNodes(self, root: Optional[TreeNode]) -> int: def depth(root): d = 0 while root: d += 1 root = root.left return d if root is None: return 0 left, right = depth(root.left), depth(root.right) if left == right: # left child subtree: (1<<left)-1 # plus root: +1 # so total except right subtree: (1<<left) return (1 << left) + self.countNodes(root.right) else: # left = right+1 return (1 << right) + self.countNodes(root.left) ############ ''' >>> 2 ** 3 8 >>> 3 ** 2 9 ''' # Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution(object): def getHeight(self, root): height = 0 while root: height += 1 root = root.left return height def countNodes(self, root): count = 0 while root: l, r = map(self.getHeight, (root.left, root.right)) if l == r: count += 2 ** l root = root.right else: count += 2 ** r root = root.left return count -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func countNodes(root *TreeNode) int { if root == nil { return 0 } left, right := depth(root.Left), depth(root.Right) if left == right { return (1 << left) + countNodes(root.Right) } return (1 << right) + countNodes(root.Left) } func depth(root *TreeNode) (d int) { for ; root != nil; root = root.Left { d++ } return } -
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number} */ var countNodes = function (root) { const depth = root => { let d = 0; for (; root; root = root.left) { ++d; } return d; }; if (!root) { return 0; } const left = depth(root.left); const right = depth(root.right); if (left == right) { return (1 << left) + countNodes(root.right); } return (1 << right) + countNodes(root.left); }; -
/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { public int CountNodes(TreeNode root) { if (root == null) { return 0; } int left = depth(root.left); int right = depth(root.right); if (left == right) { return (1 << left) + CountNodes(root.right); } return (1 << right) + CountNodes(root.left); } private int depth(TreeNode root) { int d = 0; for (; root != null; root = root.left) { ++d; } return d; } } -
use std::cell::RefCell; use std::rc::Rc; impl Solution { pub fn count_nodes(root: Option<Rc<RefCell<TreeNode>>>) -> i32 { if let Some(node) = root { let node = node.borrow(); let left = Self::depth(&node.left); let right = Self::depth(&node.right); if left == right { Self::count_nodes(node.right.clone()) + (1 << left) } else { Self::count_nodes(node.left.clone()) + (1 << right) } } else { 0 } } fn depth(root: &Option<Rc<RefCell<TreeNode>>>) -> i32 { if let Some(node) = root { Self::depth(&node.borrow().left) + 1 } else { 0 } } }