Question

Formatted question description: https://leetcode.ca/all/173.html

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):

BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.
int next() Moves the pointer to the right, then returns the number at the pointer.

Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.

You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called.

Example 1:

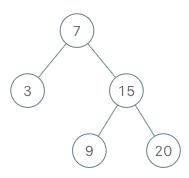
Input
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
Output
[null, 3, 7, true, 9, true, 15, true, 20, false]

Explanation
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); // return 3
bSTIterator.next(); // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next(); // return 20
bSTIterator.hasNext(); // return False

Constraints:

The number of nodes in the tree is in the range [1, 10⁵].
0 <= Node.val <= 10⁶
At most 10⁵ calls will be made to hasNext, and next.

Follow up:

Could you implement next() and hasNext() to run in average O(1) time and use O(h) memory, where h is the height of the tree?

Algorithm

The non-recursive form of the in-order traversal of the binary tree requires an additional definition of a stack to assist. The building rule of the binary search tree is left<root<right, and the in-order traversal can extract all nodes from small to large.

Code

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Stack;

public class Binary_Search_Tree_Iterator {

    /**
     * Definition for binary tree
     * public class TreeNode {
     *     int val;
     *     TreeNode left;
     *     TreeNode right;
     *     TreeNode(int x) { val = x; }
     * }
     */
    public class BSTIterator {

        Stack<TreeNode> sk;

        // @note:@memorize: important feature, min is always going left branch to leaf
        public BSTIterator(TreeNode root) {
            sk = new Stack<>();

            // all the way to leftmost leaf
            while (root != null) {
                sk.push(root);
                root = root.left;
            }

        }

        /** @return whether we have a next smallest number */
        public boolean hasNext() {
            return !sk.isEmpty();
        }

        /** @return the next smallest number */
        public int next() {
            TreeNode minNode = sk.pop();

            TreeNode current = minNode;
            // update stack, possible next time min is frmo its right-then-left branch
            if (current.right != null) {
                current = current.right;

                // same logic as in constructor
                while (current != null) {
                    sk.push(current.left);
                    current = current.left;
                }
            }

            return minNode.val;
        }
    }

/**
 * Your BSTIterator will be called like this:
 * BSTIterator i = new BSTIterator(root);
 * while (i.hasNext()) v[f()] = i.next();
 */
}

############

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class BSTIterator {
    private Deque<TreeNode> stack = new LinkedList<>();

    public BSTIterator(TreeNode root) {
        for (; root != null; root = root.left) {
            stack.offerLast(root);
        }
    }

    public int next() {
        TreeNode cur = stack.pollLast();
        for (TreeNode node = cur.right; node != null; node = node.left) {
            stack.offerLast(node);
        }
        return cur.val;
    }

    public boolean hasNext() {
        return !stack.isEmpty();
    }
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator obj = new BSTIterator(root);
 * int param_1 = obj.next();
 * boolean param_2 = obj.hasNext();
 */

// OJ: https://leetcode.com/problems/binary-search-tree-iterator/
// Time: O(1) amortized
// Space: O(H)
class BSTIterator {
private:
    stack<TreeNode*> s;
    void pushNodes(TreeNode *node) {
        while (node) {
            s.push(node);
            node = node->left;
        }
    }
public:
    BSTIterator(TreeNode* root) {
        pushNodes(root);
    }
    int next() {
        auto node = s.top();
        s.pop();
        pushNodes(node->right);
        return node->val;
    }
    bool hasNext() {
        return s.size();
    }
};

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class BSTIterator:
    def __init__(self, root: TreeNode):
        self.stack = []
        self._leftmost_inorder(root)

    def _leftmost_inorder(self, node):
        while node:
            self.stack.append(node)
            node = node.left

    def next(self) -> int:
        cur = self.stack.pop()
        node = cur.right
        self._leftmost_inorder(node)
        return cur.val

    def hasNext(self) -> bool:
        return len(self.stack) > 0

# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()

#############

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class BSTIterator:
    def __init__(self, root: TreeNode):
        self.stack = []
        while root:
            self.stack.append(root)
            root = root.left

    def next(self) -> int:
        cur = self.stack.pop()
        node = cur.right
        while node: # deplicated while block
            self.stack.append(node)
            node = node.left 
        return cur.val

    def hasNext(self) -> bool:
        return len(self.stack) > 0


# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
type BSTIterator struct {
	stack []*TreeNode
}

func Constructor(root *TreeNode) BSTIterator {
	var stack []*TreeNode
	for ; root != nil; root = root.Left {
		stack = append(stack, root)
	}
	return BSTIterator{
		stack: stack,
	}
}

func (this *BSTIterator) Next() int {
	cur := this.stack[len(this.stack)-1]
	this.stack = this.stack[:len(this.stack)-1]
	for node := cur.Right; node != nil; node = node.Left {
		this.stack = append(this.stack, node)
	}
	return cur.Val
}

func (this *BSTIterator) HasNext() bool {
	return len(this.stack) > 0
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * obj := Constructor(root);
 * param_1 := obj.Next();
 * param_2 := obj.HasNext();
 */

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

class BSTIterator {
    private stack: TreeNode[];

    constructor(root: TreeNode | null) {
        this.stack = [];
        const dfs = (root: TreeNode | null) => {
            if (root == null) {
                return;
            }
            this.stack.push(root);
            dfs(root.left);
        };
        dfs(root);
    }

    next(): number {
        const { val, right } = this.stack.pop();
        if (right) {
            let cur = right;
            while (cur != null) {
                this.stack.push(cur);
                cur = cur.left;
            }
        }
        return val;
    }

    hasNext(): boolean {
        return this.stack.length !== 0;
    }
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * var obj = new BSTIterator(root)
 * var param_1 = obj.next()
 * var param_2 = obj.hasNext()
 */

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 */
var BSTIterator = function (root) {
    this.stack = [];
    for (; root != null; root = root.left) {
        this.stack.push(root);
    }
};

/**
 * @return {number}
 */
BSTIterator.prototype.next = function () {
    let cur = this.stack.pop();
    let node = cur.right;
    for (; node != null; node = node.left) {
        this.stack.push(node);
    }
    return cur.val;
};

/**
 * @return {boolean}
 */
BSTIterator.prototype.hasNext = function () {
    return this.stack.length > 0;
};

/**
 * Your BSTIterator object will be instantiated and called as such:
 * var obj = new BSTIterator(root)
 * var param_1 = obj.next()
 * var param_2 = obj.hasNext()
 */

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
struct BSTIterator {
    stack: Vec<Option<Rc<RefCell<TreeNode>>>>,
}

use std::rc::Rc;
use std::cell::RefCell;
/**
 * `&self` means the method takes an immutable reference.
 * If you need a mutable reference, change it to `&mut self` instead.
 */
impl BSTIterator {
    fn dfs(
        mut root: Option<Rc<RefCell<TreeNode>>>,
        stack: &mut Vec<Option<Rc<RefCell<TreeNode>>>>,
    ) {
        if root.is_some() {
            let left = root.as_mut().unwrap().borrow_mut().left.take();
            stack.push(root);
            Self::dfs(left, stack);
        }
    }

    fn new(root: Option<Rc<RefCell<TreeNode>>>) -> Self {
        let mut stack = vec![];
        Self::dfs(root, &mut stack);
        BSTIterator { stack }
    }

    fn next(&mut self) -> i32 {
        let node = self.stack.pop().unwrap().unwrap();
        let mut node = node.borrow_mut();
        if node.right.is_some() {
            Self::dfs(node.right.take(), &mut self.stack)
        }
        node.val
    }

    fn has_next(&self) -> bool {
        self.stack.len() != 0
    }
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * let obj = BSTIterator::new(root);
 * let ret_1: i32 = obj.next();
 * let ret_2: bool = obj.has_next();
 */

173 - Binary Search Tree Iterator

Question

Algorithm

Code

All Problems

All Solutions

Welcome to Subscribe On Youtube

Question

Algorithm

Code

All Problems

All Solutions