Welcome to Subscribe On Youtube
147. Insertion Sort List
Description
Given the head of a singly linked list, sort the list using insertion sort, and return the sorted list's head.
The steps of the insertion sort algorithm:
- Insertion sort iterates, consuming one input element each repetition and growing a sorted output list.
- At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list and inserts it there.
- It repeats until no input elements remain.
The following is a graphical example of the insertion sort algorithm. The partially sorted list (black) initially contains only the first element in the list. One element (red) is removed from the input data and inserted in-place into the sorted list with each iteration.
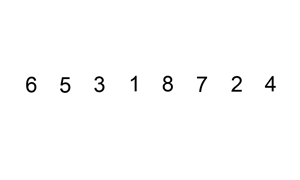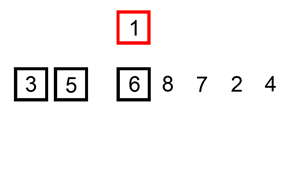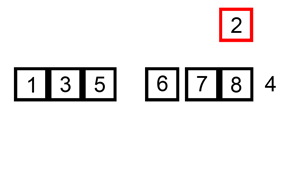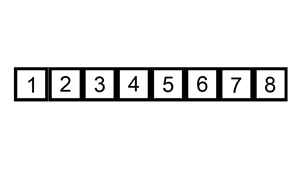
Example 1:
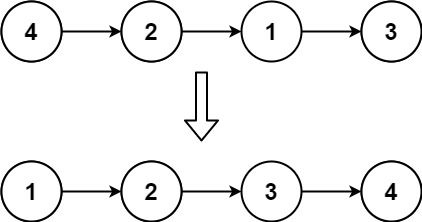
Input: head = [4,2,1,3] Output: [1,2,3,4]
Example 2:
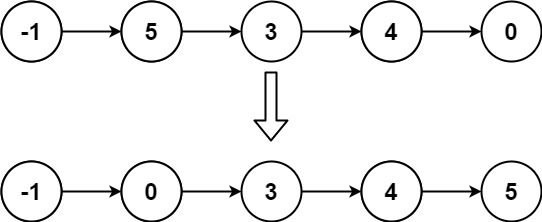
Input: head = [-1,5,3,4,0] Output: [-1,0,3,4,5]
Constraints:
- The number of nodes in the list is in the range
[1, 5000]. -5000 <= Node.val <= 5000
Solutions
Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, it has several advantages, such as simplicity and the ability to sort a list as it receives it.
Code Explanation:
-
Base Case Check: If the list is empty (
head is None) or contains only one element (head.next is None), it’s already sorted, so returnhead. -
Dummy Head Initialization: A dummy node is created and pointed to the
headof the list. This dummy node serves as an anchor and simplifies edge case handling, such as inserting elements at the head of the list. -
Iteration Setup: Two pointers,
preandcur, are initialized to help traverse the list.prestarts at the dummy node, andcurstarts at theheadof the list. The idea is to iterate through the list withcur, and for each node, find its correct position in the portion of the list beforecurthat has already been sorted. -
Main Loop: The loop continues as long as
curis notNone, indicating there are still elements to be sorted. -
Direct Append Check: If the current element pointed by
preis less than or equal tocur, it meanscuris already in the correct position relative topre, so move both pointers forward. -
Finding Insertion Point: If
curneeds to be moved to an earlier position to maintain sorting, start from the dummy node with a pointerpand move forward until finding the insertion point wherep.next.val > cur.val. This indicates thatcurshould be inserted betweenpandp.next. - Re-linking: Once the insertion point is found:
- Temporarily store
cur.nextint, as the next element to sort after reinsertingcur. - Insert
curbetweenpandp.nextby settingcur.next = p.nextandp.next = cur. - Update
pre.nexttotbecausecurhas been moved out of its original position. - Move
curtot, preparing for the next iteration.
- Temporarily store
- Return: Once all elements have been correctly positioned, return
dummy.next, which points to the head of the newly sorted list.
Important Points:
- The use of a dummy head node simplifies edge cases, especially when inserting at the beginning of the list.
- The algorithm iteratively takes each element from the unsorted portion of the list and finds its correct position in the sorted portion, effectively extending the sorted portion one element at a time.
- The while loop that moves pointer
pis crucial for maintaining the sorted order by finding the correct insertion point for each element incur.
-
/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode() {} * ListNode(int val) { this.val = val; } * ListNode(int val, ListNode next) { this.val = val; this.next = next; } * } */ class Solution { public ListNode insertionSortList(ListNode head) { if (head == null || head.next == null) { return head; } ListNode dummy = new ListNode(head.val, head); ListNode pre = dummy, cur = head; while (cur != null) { if (pre.val <= cur.val) { pre = cur; cur = cur.next; continue; } ListNode p = dummy; while (p.next.val <= cur.val) { p = p.next; } ListNode t = cur.next; cur.next = p.next; p.next = cur; pre.next = t; cur = t; } return dummy.next; } } -
# Definition for singly-linked list. # class ListNode: # def __init__(self, val=0, next=None): # self.val = val # self.next = next class Solution: def insertionSortList(self, head: ListNode) -> ListNode: if head is None or head.next is None: return head dummy = ListNode(head.val, head) pre, cur = dummy, head while cur: if pre.val <= cur.val: pre, cur = cur, cur.next continue p = dummy while p.next.val <= cur.val: p = p.next t = cur.next cur.next = p.next p.next = cur pre.next = t cur = t return dummy.next -
/** * Definition for singly-linked list. * function ListNode(val, next) { * this.val = (val===undefined ? 0 : val) * this.next = (next===undefined ? null : next) * } */ /** * @param {ListNode} head * @return {ListNode} */ var insertionSortList = function (head) { if (head == null || head.next == null) return head; let dummy = new ListNode(head.val, head); let prev = dummy, cur = head; while (cur != null) { if (prev.val <= cur.val) { prev = cur; cur = cur.next; continue; } let p = dummy; while (p.next.val <= cur.val) { p = p.next; } let t = cur.next; cur.next = p.next; p.next = cur; prev.next = t; cur = t; } return dummy.next; };