Welcome to Subscribe On Youtube
142. Linked List Cycle II
Description
Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
Example 1:

Input: head = [3,2,0,-4], pos = 1 Output: tail connects to node index 1 Explanation: There is a cycle in the linked list, where tail connects to the second node.
Example 2:
Input: head = [1,2], pos = 0 Output: tail connects to node index 0 Explanation: There is a cycle in the linked list, where tail connects to the first node.
Example 3:

Input: head = [1], pos = -1 Output: no cycle Explanation: There is no cycle in the linked list.
Constraints:
- The number of the nodes in the list is in the range
[0, 104]. -105 <= Node.val <= 105posis-1or a valid index in the linked-list.
Follow up: Can you solve it using O(1) (i.e. constant) memory?
Solutions
Solution 1: Two Pointers
We first use the fast and slow pointers to judge whether the linked list has a ring. If there is a ring, the fast and slow pointers will definitely meet, and the meeting node must be in the ring.
If there is no ring, the fast pointer will reach the tail of the linked list first, and return null directly.
If there is a ring, we then define an answer pointer $ans$ to point to the head of the linked list, and then let $ans$ and the slow pointer move forward together, moving one step at a time, until $ans$ and the slow pointer meet, and the meeting node is the ring entrance node.
Why can this find the entrance node of the ring?
Let’s assume that the distance from the head node of the linked list to the entrance of the ring is $x$, the distance from the entrance of the ring to the meeting node is $y$, and the distance from the meeting node to the entrance of the ring is $z$. Then the distance traveled by the slow pointer is $x + y$, and the distance traveled by the fast pointer is $x + y + k \times (y + z)$, where $k$ is the number of times the fast pointer goes around the ring.
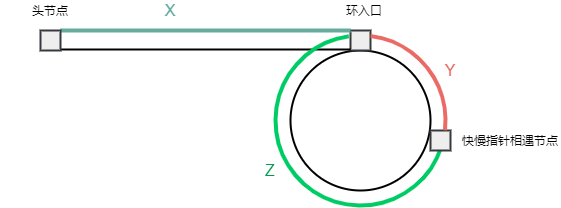
Because the speed of the fast pointer is twice that of the slow pointer, it is $2 \times (x + y) = x + y + k \times (y + z)$, which can be deduced that $x + y = k \times (y + z)$, that is $x = (k - 1) \times (y + z) + z$.
That is to say, if we define an answer pointer $ans$ to point to the head of the linked list, and the $ans$ and the slow pointer move forward together, they will definitely meet at the ring entrance.
The time complexity is $O(n)$, where $n$ is the number of nodes in the linked list. The space complexity is $O(1)$.
Math prove:
a b
A ------ B --------+
| |
c | |
C --------+
* A: 起始点
* B: Cycle Begins
* C: 1st 快慢指针相遇点
* A->B: a
* B->C: b
* C->B: c
* 环的长度 (b+c) 为 R
To understand this solution, you just need to ask yourself these question.
Assume the distance from head to the start of the loop is a
the distance from the start of the loop to the point fast and slow meet is b
the distance from the point fast and slow meet to the start of the loop is c
- What is the distance fast moved?
- What is the distance slow moved?
- And their relationship?
fast: a + b + c + b
slow: a + b
relationship - fast is 2X faster than slow: a + b + c + b = 2 * (a + b)
Thus a = c
-
/** * Definition for singly-linked list. * class ListNode { * int val; * ListNode next; * ListNode(int x) { * val = x; * next = null; * } * } */ public class Solution { public ListNode detectCycle(ListNode head) { ListNode fast = head, slow = head; while (fast != null && fast.next != null) { slow = slow.next; fast = fast.next.next; if (slow == fast) { ListNode ans = head; while (ans != slow) { ans = ans.next; slow = slow.next; } return ans; } } return null; } } -
/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode(int x) : val(x), next(NULL) {} * }; */ class Solution { public: ListNode* detectCycle(ListNode* head) { ListNode* fast = head; ListNode* slow = head; while (fast && fast->next) { slow = slow->next; fast = fast->next->next; if (slow == fast) { ListNode* ans = head; while (ans != slow) { ans = ans->next; slow = slow->next; } return ans; } } return nullptr; } }; -
# Definition for singly-linked list. # class ListNode: # def __init__(self, x): # self.val = x # self.next = None class Solution: def detectCycle(self, head: ListNode) -> ListNode: slow = fast = head has_cycle = False while not has_cycle and fast and fast.next: slow, fast = slow.next, fast.next.next has_cycle = slow == fast if not has_cycle: return None p = head while p != slow: p, slow = p.next, slow.next return p ############# class Solution: def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]: fast = slow = head while fast and fast.next: slow = slow.next fast = fast.next.next if slow == fast: ans = head while ans != slow: ans = ans.next slow = slow.next return ans -
/** * Definition for singly-linked list. * type ListNode struct { * Val int * Next *ListNode * } */ func detectCycle(head *ListNode) *ListNode { fast, slow := head, head for fast != nil && fast.Next != nil { slow = slow.Next fast = fast.Next.Next if slow == fast { ans := head for ans != slow { ans = ans.Next slow = slow.Next } return ans } } return nil } -
/** * Definition for singly-linked list. * class ListNode { * val: number * next: ListNode | null * constructor(val?: number, next?: ListNode | null) { * this.val = (val===undefined ? 0 : val) * this.next = (next===undefined ? null : next) * } * } */ function detectCycle(head: ListNode | null): ListNode | null { let [slow, fast] = [head, head]; while (fast && fast.next) { slow = slow.next; fast = fast.next.next; if (slow === fast) { let ans = head; while (ans !== slow) { ans = ans.next; slow = slow.next; } return ans; } } return null; } -
/** * Definition for singly-linked list. * function ListNode(val) { * this.val = val; * this.next = null; * } */ /** * @param {ListNode} head * @return {ListNode} */ var detectCycle = function (head) { let [slow, fast] = [head, head]; while (fast && fast.next) { slow = slow.next; fast = fast.next.next; if (slow === fast) { let ans = head; while (ans !== slow) { ans = ans.next; slow = slow.next; } return ans; } } return null; };