Welcome to Subscribe On Youtube
129. Sum Root to Leaf Numbers
Description
You are given the root of a binary tree containing digits from 0 to 9 only.
Each root-to-leaf path in the tree represents a number.
- For example, the root-to-leaf path
1 -> 2 -> 3represents the number123.
Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.
A leaf node is a node with no children.
Example 1:
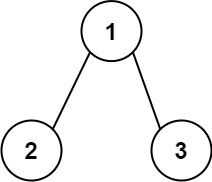
Input: root = [1,2,3] Output: 25 Explanation: The root-to-leaf path1->2represents the number12. The root-to-leaf path1->3represents the number13. Therefore, sum = 12 + 13 =25.
Example 2:
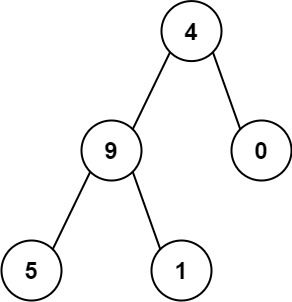
Input: root = [4,9,0,5,1] Output: 1026 Explanation: The root-to-leaf path4->9->5represents the number 495. The root-to-leaf path4->9->1represents the number 491. The root-to-leaf path4->0represents the number 40. Therefore, sum = 495 + 491 + 40 =1026.
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. 0 <= Node.val <= 9- The depth of the tree will not exceed
10.
Solutions
Solution 1: DFS
We can design a function $dfs(root, s)$, which represents the sum of all path numbers from the current node $root$ to the leaf nodes, given that the current path number is $s$. The answer is $dfs(root, 0)$.
The calculation of the function $dfs(root, s)$ is as follows:
- If the current node $root$ is null, return $0$.
- Otherwise, add the value of the current node to $s$, i.e., $s = s \times 10 + root.val$.
- If the current node is a leaf node, return $s$.
- Otherwise, return $dfs(root.left, s) + dfs(root.right, s)$.
The time complexity is $O(n)$, and the space complexity is $O(\log n)$. Here, $n$ is the number of nodes in the binary tree.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public int sumNumbers(TreeNode root) { return dfs(root, 0); } private int dfs(TreeNode root, int s) { if (root == null) { return 0; } s = s * 10 + root.val; if (root.left == null && root.right == null) { return s; } return dfs(root.left, s) + dfs(root.right, s); } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int sumNumbers(TreeNode* root) { function<int(TreeNode*, int)> dfs = [&](TreeNode* root, int s) -> int { if (!root) return 0; s = s * 10 + root->val; if (!root->left && !root->right) return s; return dfs(root->left, s) + dfs(root->right, s); }; return dfs(root, 0); } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def sumNumbers(self, root: Optional[TreeNode]) -> int: def dfs(root, s): if root is None: return 0 s = s * 10 + root.val if root.left is None and root.right is None: return s return dfs(root.left, s) + dfs(root.right, s) return dfs(root, 0) -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func sumNumbers(root *TreeNode) int { var dfs func(*TreeNode, int) int dfs = func(root *TreeNode, s int) int { if root == nil { return 0 } s = s*10 + root.Val if root.Left == nil && root.Right == nil { return s } return dfs(root.Left, s) + dfs(root.Right, s) } return dfs(root, 0) } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function sumNumbers(root: TreeNode | null): number { function dfs(root: TreeNode | null, s: number): number { if (!root) return 0; s = s * 10 + root.val; if (!root.left && !root.right) return s; return dfs(root.left, s) + dfs(root.right, s); } return dfs(root, 0); } -
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number} */ var sumNumbers = function (root) { function dfs(root, s) { if (!root) return 0; s = s * 10 + root.val; if (!root.left && !root.right) return s; return dfs(root.left, s) + dfs(root.right, s); } return dfs(root, 0); }; -
// Definition for a binary tree node. // #[derive(Debug, PartialEq, Eq)] // pub struct TreeNode { // pub val: i32, // pub left: Option<Rc<RefCell<TreeNode>>>, // pub right: Option<Rc<RefCell<TreeNode>>>, // } // // impl TreeNode { // #[inline] // pub fn new(val: i32) -> Self { // TreeNode { // val, // left: None, // right: None // } // } // } use std::rc::Rc; use std::cell::RefCell; impl Solution { fn dfs(node: &Option<Rc<RefCell<TreeNode>>>, mut num: i32) -> i32 { if node.is_none() { return 0; } let node = node.as_ref().unwrap().borrow(); num = num * 10 + node.val; if node.left.is_none() && node.right.is_none() { return num; } Self::dfs(&node.left, num) + Self::dfs(&node.right, num) } pub fn sum_numbers(root: Option<Rc<RefCell<TreeNode>>>) -> i32 { Self::dfs(&root, 0) } }