Welcome to Subscribe On Youtube
130. Surrounded Regions
Description
Given an m x n matrix board containing 'X' and 'O', capture all regions that are 4-directionally surrounded by 'X'.
A region is captured by flipping all 'O's into 'X's in that surrounded region.
Example 1:
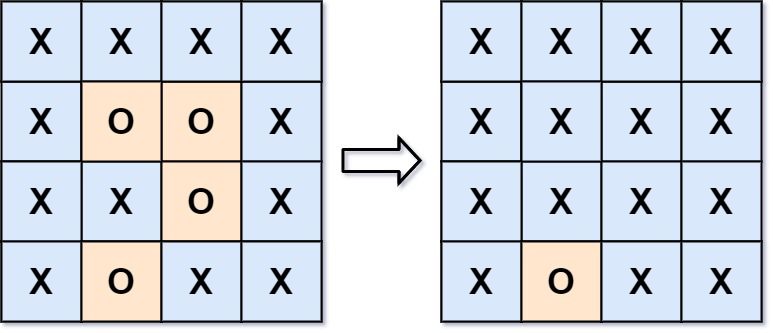
Input: board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]] Output: [["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]] Explanation: Notice that an 'O' should not be flipped if: - It is on the border, or - It is adjacent to an 'O' that should not be flipped. The bottom 'O' is on the border, so it is not flipped. The other three 'O' form a surrounded region, so they are flipped.
Example 2:
Input: board = [["X"]] Output: [["X"]]
Constraints:
m == board.lengthn == board[i].length1 <= m, n <= 200board[i][j]is'X'or'O'.
Solutions
-
class Solution { private char[][] board; private int m; private int n; public void solve(char[][] board) { m = board.length; n = board[0].length; this.board = board; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if ((i == 0 || i == m - 1 || j == 0 || j == n - 1) && board[i][j] == 'O') { dfs(i, j); } } } for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (board[i][j] == '.') { board[i][j] = 'O'; } else if (board[i][j] == 'O') { board[i][j] = 'X'; } } } } private void dfs(int i, int j) { board[i][j] = '.'; int[] dirs = {-1, 0, 1, 0, -1}; for (int k = 0; k < 4; ++k) { int x = i + dirs[k]; int y = j + dirs[k + 1]; if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O') { dfs(x, y); } } } } -
class Solution { public: void solve(vector<vector<char>>& board) { int m = board.size(), n = board[0].size(); for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) if ((i == 0 || i == m - 1 || j == 0 || j == n - 1) && board[i][j] == 'O') dfs(board, i, j); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (board[i][j] == '.') board[i][j] = 'O'; else if (board[i][j] == 'O') board[i][j] = 'X'; } } } void dfs(vector<vector<char>>& board, int i, int j) { board[i][j] = '.'; vector<int> dirs = {-1, 0, 1, 0, -1}; for (int k = 0; k < 4; ++k) { int x = i + dirs[k], y = j + dirs[k + 1]; if (x >= 0 && x < board.size() && y >= 0 && y < board[0].size() && board[x][y] == 'O') dfs(board, x, y); } } }; -
class Solution: def solve(self, board: List[List[str]]) -> None: """ Do not return anything, modify board in-place instead. """ def dfs(i, j): board[i][j] = '.' for a, b in [[0, -1], [0, 1], [1, 0], [-1, 0]]: x, y = i + a, j + b if 0 <= x < m and 0 <= y < n and board[x][y] == 'O': dfs(x, y) m, n = len(board), len(board[0]) for i in range(m): for j in range(n): if board[i][j] == 'O' and ( i == 0 or i == m - 1 or j == 0 or j == n - 1 ): dfs(i, j) for i in range(m): for j in range(n): if board[i][j] == 'O': board[i][j] = 'X' elif board[i][j] == '.': board[i][j] = 'O' -
func solve(board [][]byte) { m, n := len(board), len(board[0]) var dfs func(i, j int) dfs = func(i, j int) { board[i][j] = '.' dirs := []int{-1, 0, 1, 0, -1} for k := 0; k < 4; k++ { x, y := i+dirs[k], j+dirs[k+1] if x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O' { dfs(x, y) } } } for i := 0; i < m; i++ { for j := 0; j < n; j++ { if (i == 0 || i == m-1 || j == 0 || j == n-1) && board[i][j] == 'O' { dfs(i, j) } } } for i := 0; i < m; i++ { for j := 0; j < n; j++ { if board[i][j] == '.' { board[i][j] = 'O' } else if board[i][j] == 'O' { board[i][j] = 'X' } } } } -
/** Do not return anything, modify board in-place instead. */ function solve(board: string[][]): void { function dfs(i, j) { board[i][j] = '.'; const dirs = [-1, 0, 1, 0, -1]; for (let k = 0; k < 4; ++k) { const x = i + dirs[k]; const y = j + dirs[k + 1]; if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O') { dfs(x, y); } } } const m = board.length; const n = board[0].length; for (let i = 0; i < m; ++i) { for (let j = 0; j < n; ++j) { if ((i == 0 || i == m - 1 || j == 0 || j == n - 1) && board[i][j] == 'O') { dfs(i, j); } } } for (let i = 0; i < m; ++i) { for (let j = 0; j < n; ++j) { if (board[i][j] == '.') { board[i][j] = 'O'; } else if (board[i][j] == 'O') { board[i][j] = 'X'; } } } } -
using System; using System.Collections.Generic; public class Solution { private static readonly int[,] directions = new int[4, 2] { { 1, 0 }, { 0, 1 }, { -1, 0 }, { 0, -1 } }; public void Solve(char[][] board) { var lenI = board.Length; var lenJ = lenI == 0 ? 0 : board[0].Length; for (var i = 0; i < lenI; ++i) { for (var j = 0; j < lenJ; ++j) { if (board[i][j] == 'O') { var marked = new List<Tuple<int, int>>(); marked.Add(Tuple.Create(i, j)); board[i][j] = 'M'; bool escaped = false; for (var m = 0; m < marked.Count; ++m) { for (var k = 0; k < 4; ++k) { var newI = marked[m].Item1 + directions[k, 0]; var newJ = marked[m].Item2 + directions[k, 1]; if (newI < 0 || newI >= lenI || newJ < 0 || newJ >= lenJ) { escaped = true; } else if (board[newI][newJ] == 'O') { board[newI][newJ] = 'M'; marked.Add(Tuple.Create(newI, newJ)); } } } if (!escaped) { foreach (var item in marked) { board[item.Item1][item.Item2] = 'X'; } } } } } for (var i = 0; i < lenI; ++i) { for (var j = 0; j < lenJ; ++j) { if (board[i][j] == 'M') { board[i][j] = 'O'; } } } } } -
impl Solution { fn dfs(i: usize, j: usize, mark: char, vis: &mut Vec<Vec<bool>>, board: &mut Vec<Vec<char>>) { if vis[i][j] || board[i][j] != mark { return; } vis[i][j] = true; if i > 0 { Self::dfs(i - 1, j, mark, vis, board); } if i < vis.len() - 1 { Self::dfs(i + 1, j, mark, vis, board); } if j > 0 { Self::dfs(i, j - 1, mark, vis, board); } if j < vis[0].len() - 1 { Self::dfs(i, j + 1, mark, vis, board); } } pub fn solve(board: &mut Vec<Vec<char>>) { let m = board.len(); let n = board[0].len(); let mut vis = vec![vec![false; n]; m]; for i in 0..m { Self::dfs(i, 0, board[i][0], &mut vis, board); Self::dfs(i, n - 1, board[i][n - 1], &mut vis, board); } for i in 0..n { Self::dfs(0, i, board[0][i], &mut vis, board); Self::dfs(m - 1, i, board[m - 1][i], &mut vis, board); } for i in 0..m { for j in 0..n { if vis[i][j] { continue; } board[i][j] = 'X'; } } } }