Welcome to Subscribe On Youtube
124. Binary Tree Maximum Path Sum
Description
A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
The path sum of a path is the sum of the node's values in the path.
Given the root of a binary tree, return the maximum path sum of any non-empty path.
Example 1:
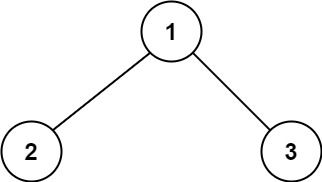
Input: root = [1,2,3] Output: 6 Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
Example 2:
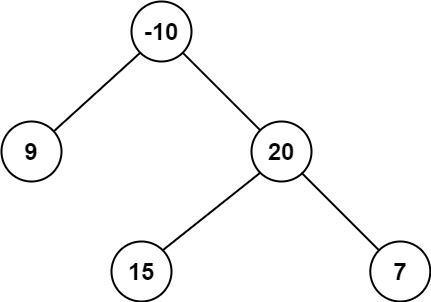
Input: root = [-10,9,20,null,null,15,7] Output: 42 Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
Constraints:
- The number of nodes in the tree is in the range
[1, 3 * 104]. -1000 <= Node.val <= 1000
Solutions
Solution 1: Recursion
When thinking about the classic routine of recursion problems in binary trees, we consider:
- Termination condition (when to terminate recursion)
- Recursively process the left and right subtrees
- Merge the calculation results of the left and right subtrees
For this problem, we design a function $dfs(root)$, which returns the maximum path sum of the binary tree with $root$ as the root node.
The execution logic of the function $dfs(root)$ is as follows:
If $root$ does not exist, then $dfs(root)$ returns $0$;
Otherwise, we recursively calculate the maximum path sum of the left and right subtrees of $root$, denoted as $left$ and $right$. If $left$ is less than $0$, then we set it to $0$, similarly, if $right$ is less than $0$, then we set it to $0$.
Then, we update the answer with $root.val + left + right$. Finally, the function returns $root.val + \max(left, right)$.
In the main function, we call $dfs(root)$ to get the maximum path sum of each node, and the maximum value among them is the answer.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { private int ans = -1001; public int maxPathSum(TreeNode root) { dfs(root); return ans; } private int dfs(TreeNode root) { if (root == null) { return 0; } int left = Math.max(0, dfs(root.left)); int right = Math.max(0, dfs(root.right)); ans = Math.max(ans, root.val + left + right); return root.val + Math.max(left, right); } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int maxPathSum(TreeNode* root) { int ans = -1001; function<int(TreeNode*)> dfs = [&](TreeNode* root) { if (!root) { return 0; } int left = max(0, dfs(root->left)); int right = max(0, dfs(root->right)); ans = max(ans, left + right + root->val); return root->val + max(left, right); }; dfs(root); return ans; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def maxPathSum(self, root: Optional[TreeNode]) -> int: def dfs(root: Optional[TreeNode]) -> int: if root is None: return 0 left = max(0, dfs(root.left)) right = max(0, dfs(root.right)) nonlocal ans ans = max(ans, root.val + left + right) return root.val + max(left, right) ans = -inf dfs(root) return ans -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func maxPathSum(root *TreeNode) int { ans := -1001 var dfs func(*TreeNode) int dfs = func(root *TreeNode) int { if root == nil { return 0 } left := max(0, dfs(root.Left)) right := max(0, dfs(root.Right)) ans = max(ans, left+right+root.Val) return max(left, right) + root.Val } dfs(root) return ans } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function maxPathSum(root: TreeNode | null): number { let ans = -1001; const dfs = (root: TreeNode | null): number => { if (!root) { return 0; } const left = Math.max(0, dfs(root.left)); const right = Math.max(0, dfs(root.right)); ans = Math.max(ans, left + right + root.val); return Math.max(left, right) + root.val; }; dfs(root); return ans; } -
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number} */ var maxPathSum = function (root) { let ans = -1001; const dfs = root => { if (!root) { return 0; } const left = Math.max(0, dfs(root.left)); const right = Math.max(0, dfs(root.right)); ans = Math.max(ans, left + right + root.val); return Math.max(left, right) + root.val; }; dfs(root); return ans; }; -
/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { private int ans = -1001; public int MaxPathSum(TreeNode root) { dfs(root); return ans; } private int dfs(TreeNode root) { if (root == null) { return 0; } int left = Math.Max(0, dfs(root.left)); int right = Math.Max(0, dfs(root.right)); ans = Math.Max(ans, left + right + root.val); return root.val + Math.Max(left, right); } } -
// Definition for a binary tree node. // #[derive(Debug, PartialEq, Eq)] // pub struct TreeNode { // pub val: i32, // pub left: Option<Rc<RefCell<TreeNode>>>, // pub right: Option<Rc<RefCell<TreeNode>>>, // } // // impl TreeNode { // #[inline] // pub fn new(val: i32) -> Self { // TreeNode { // val, // left: None, // right: None // } // } // } use std::rc::Rc; use std::cell::RefCell; impl Solution { fn dfs(root: &Option<Rc<RefCell<TreeNode>>>, res: &mut i32) -> i32 { if root.is_none() { return 0; } let node = root.as_ref().unwrap().borrow(); let left = (0).max(Self::dfs(&node.left, res)); let right = (0).max(Self::dfs(&node.right, res)); *res = (node.val + left + right).max(*res); node.val + left.max(right) } pub fn max_path_sum(root: Option<Rc<RefCell<TreeNode>>>) -> i32 { let mut res = -1000; Self::dfs(&root, &mut res); res } }