Welcome to Subscribe On Youtube
116. Populating Next Right Pointers in Each Node
Description
You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Example 1:
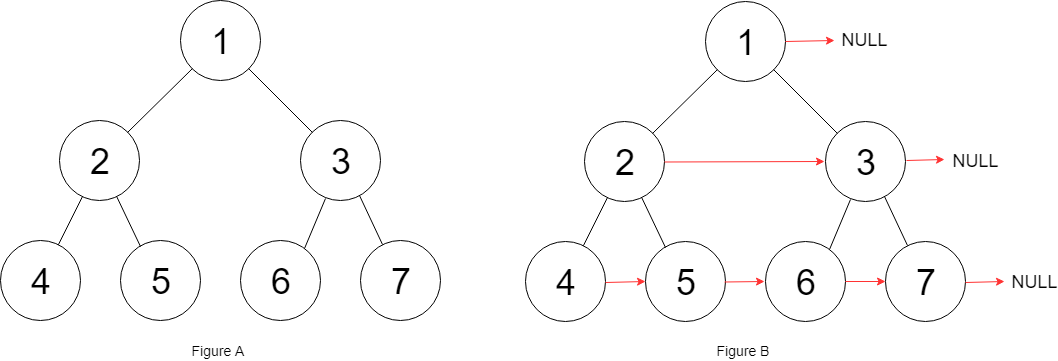
Input: root = [1,2,3,4,5,6,7] Output: [1,#,2,3,#,4,5,6,7,#] Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
Example 2:
Input: root = [] Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 212 - 1]. -1000 <= Node.val <= 1000
Follow-up:
- You may only use constant extra space.
- The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.
Solutions
Solution 1: BFS
Use a queue for level order traversal, and each time you traverse a level, connect the nodes of the current level in order.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree.
Solution 2: DFS
Use recursion for preorder traversal, and each time you traverse to a node, connect its left and right child nodes in order.
Specifically, we design a function $dfs(left, right)$, which points the $next$ pointer of the $left$ node to the $right$ node. In the function, we first check whether $left$ and $right$ are null. If both are not null, point $left.next$ to $right$, and then recursively call $dfs(left.left, left.right)$, $dfs(left.right, right.left)$, $dfs(right.left, right.right)$.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree.
-
/* // Definition for a Node. class Node { public int val; public Node left; public Node right; public Node next; public Node() {} public Node(int _val) { val = _val; } public Node(int _val, Node _left, Node _right, Node _next) { val = _val; left = _left; right = _right; next = _next; } }; */ class Solution { public Node connect(Node root) { if (root == null) { return root; } Deque<Node> q = new ArrayDeque<>(); q.offer(root); while (!q.isEmpty()) { Node p = null; for (int n = q.size(); n > 0; --n) { Node node = q.poll(); if (p != null) { p.next = node; } p = node; if (node.left != null) { q.offer(node.left); } if (node.right != null) { q.offer(node.right); } } } return root; } } -
/* // Definition for a Node. class Node { public: int val; Node* left; Node* right; Node* next; Node() : val(0), left(NULL), right(NULL), next(NULL) {} Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {} Node(int _val, Node* _left, Node* _right, Node* _next) : val(_val), left(_left), right(_right), next(_next) {} }; */ class Solution { public: Node* connect(Node* root) { if (!root) { return root; } queue<Node*> q{ {root} }; while (!q.empty()) { Node* p = nullptr; for (int n = q.size(); n; --n) { Node* node = q.front(); q.pop(); if (p) { p->next = node; } p = node; if (node->left) { q.push(node->left); } if (node->right) { q.push(node->right); } } } return root; } }; -
""" # Definition for a Node. class Node: def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None): self.val = val self.left = left self.right = right self.next = next """ ''' >>> d = deque((5,1,9,2)) >>> d.popleft() 5 >>> d.popleft() 1 >>> >>> >>> d = deque([5,1,9,2]) >>> d.popleft() 5 >>> d.popleft() 1 ''' from collections import deque class Solution: def connect(self, root: "Optional[Node]") -> "Optional[Node]": if root is None: return root # q = deque(root) ===> TypeError: 'Node' object is not iterable # make it a list [], so it's iterable q = deque([root]) while q: prev = None for _ in range(len(q)): node = q.popleft() if prev: p.next = node prev = node if node.left: q.append(node.left) if node.right: q.append(node.right) return root class Solution: def connect(self, root: 'Node') -> 'Node': if not root: return root l = [root] # list while l: size = len(l) for i in range(size): node = l.pop(0) # pop() is last, pop(0) is first of list if i < size - 1: node.next = l[0] if node.left: l.append(node.left) if node.right: l.append(node.right) return root # recursion class Solution: def connect(self, root: "Optional[Node]") -> "Optional[Node]": self._connect(root, None) return root def _connect(self, current: 'Optional[Node]', next_node: 'Optional[Node]') -> None: if current is None: return else: current.next = next_node # connect self._connect(current.left, current.right) if next_node is not None: self._connect(current.right, next_node.left) else: self._connect(current.right, None) -
/** * Definition for a Node. * type Node struct { * Val int * Left *Node * Right *Node * Next *Node * } */ func connect(root *Node) *Node { if root == nil { return root } q := []*Node{root} for len(q) > 0 { var p *Node for n := len(q); n > 0; n-- { node := q[0] q = q[1:] if p != nil { p.Next = node } p = node if node.Left != nil { q = append(q, node.Left) } if node.Right != nil { q = append(q, node.Right) } } } return root } -
/** * Definition for Node. * class Node { * val: number * left: Node | null * right: Node | null * next: Node | null * constructor(val?: number, left?: Node, right?: Node, next?: Node) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * this.next = (next===undefined ? null : next) * } * } */ function connect(root: Node | null): Node | null { if (root == null || root.left == null) { return root; } const { left, right, next } = root; left.next = right; if (next != null) { right.next = next.left; } connect(left); connect(right); return root; }