114. Flatten Binary Tree to Linked List

Description

Given the root of a binary tree, flatten the tree into a "linked list":

The "linked list" should use the same TreeNode class where the right child pointer points to the next node in the list and the left child pointer is always null.
The "linked list" should be in the same order as a pre-order traversal of the binary tree.

Example 1:

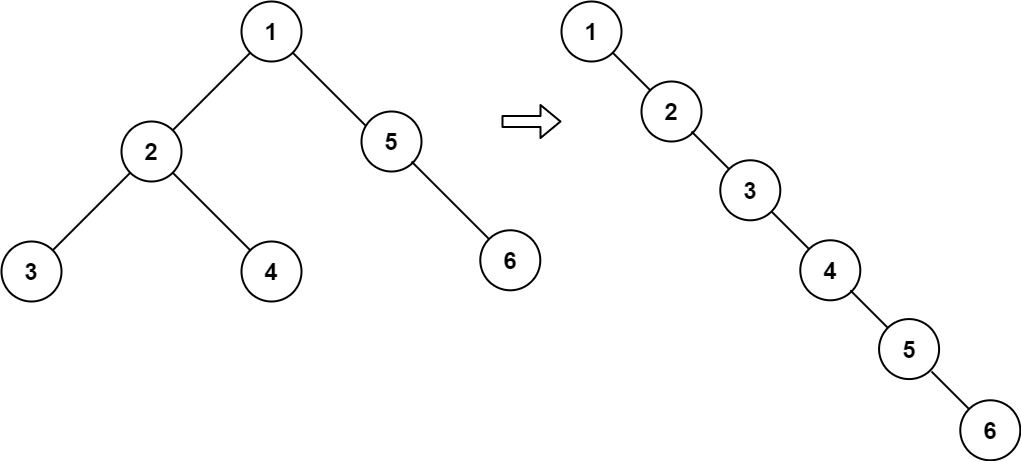
Input: root = [1,2,5,3,4,null,6]
Output: [1,null,2,null,3,null,4,null,5,null,6]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [0]
Output: [0]

Constraints:

The number of nodes in the tree is in the range [0, 2000].
-100 <= Node.val <= 100

Follow up: Can you flatten the tree in-place (with O(1) extra space)?

Solutions

Solution 1: Find Predecessor Node

The visit order of preorder traversal is “root, left subtree, right subtree”. After the last node of the left subtree is visited, the right subtree node of the root node will be visited next.

Therefore, for the current node, if its left child node is not null, we find the rightmost node of the left subtree as the predecessor node, and then assign the right child node of the current node to the right child node of the predecessor node. Then assign the left child node of the current node to the right child node of the current node, and set the left child node of the current node to null. Then take the right child node of the current node as the next node and continue processing until all nodes are processed.

The time complexity is $O(n)$, where $n$ is the number of nodes in the tree. The space complexity is $O(1)$.

Flatten process:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public void flatten(TreeNode root) {
        while (root != null) {
            if (root.left != null) {
                TreeNode pre = root.left;
                while (pre.right != null) {
                    pre = pre.right;
                }
                pre.right = root.right;
                root.right = root.left;
                root.left = null;
            }
            root = root.right;
        }
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        while (root) {
            if (root->left) {
                TreeNode* pre = root->left;
                while (pre->right) {
                    pre = pre->right;
                }
                pre->right = root->right;
                root->right = root->left;
                root->left = nullptr;
            }
            root = root->right;
        }
    }
};

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution: # stack, pre-order interation
    def flatten(self, root: TreeNode) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        if not root:
            return
        
        stack = [root]
        prev = TreeNode(0) # dummy node
        
        while stack:
            current = stack.pop()
            
            if current.right:
                stack.append(current.right)
            if current.left:
                stack.append(current.left)
                
            prev.left = None
            prev.right = current
            
            prev = current

###########

class Solution: # no stack
    def flatten(self, root: Optional[TreeNode]) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        while root:
            if root.left:
                pre = root.left
                while pre.right: # start feom right
                    pre = pre.right
                pre.right = root.right
                root.right = root.left
                root.left = None
            root = root.right

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func flatten(root *TreeNode) {
	for root != nil {
		left, right := root.Left, root.Right
		root.Left = nil
		if left != nil {
			root.Right = left
			for left.Right != nil {
				left = left.Right
			}
			left.Right = right
		}
		root = root.Right
	}
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

/**
 Do not return anything, modify root in-place instead.
 */
function flatten(root: TreeNode | null): void {
    while (root !== null) {
        if (root.left !== null) {
            let pre = root.left;
            while (pre.right !== null) {
                pre = pre.right;
            }
            pre.right = root.right;
            root.right = root.left;
            root.left = null;
        }
        root = root.right;
    }
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var flatten = function (root) {
    while (root) {
        if (root.left) {
            let pre = root.left;
            while (pre.right) {
                pre = pre.right;
            }
            pre.right = root.right;
            root.right = root.left;
            root.left = null;
        }
        root = root.right;
    }
};

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    #[allow(dead_code)]
    pub fn flatten(root: &mut Option<Rc<RefCell<TreeNode>>>) {
        if root.is_none() {
            return;
        }
        let mut v: Vec<Option<Rc<RefCell<TreeNode>>>> = Vec::new();
        // Initialize the vector
        Self::pre_order_traverse(&mut v, root);
        // Traverse the vector
        let n = v.len();
        for i in 0..n - 1 {
            v[i].as_ref().unwrap().borrow_mut().left = None;
            v[i].as_ref().unwrap().borrow_mut().right = v[i + 1].clone();
        }
    }

    #[allow(dead_code)]
    fn pre_order_traverse(
        v: &mut Vec<Option<Rc<RefCell<TreeNode>>>>,
        root: &Option<Rc<RefCell<TreeNode>>>
    ) {
        if root.is_none() {
            return;
        }
        v.push(root.clone());
        let left = root.as_ref().unwrap().borrow().left.clone();
        let right = root.as_ref().unwrap().borrow().right.clone();
        Self::pre_order_traverse(v, &left);
        Self::pre_order_traverse(v, &right);
    }
}

114 - Flatten Binary Tree to Linked List

114. Flatten Binary Tree to Linked List

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

114. Flatten Binary Tree to Linked List

Description

Solutions

All Problems

All Solutions