108. Convert Sorted Array to Binary Search Tree

Description

Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.

Example 1:

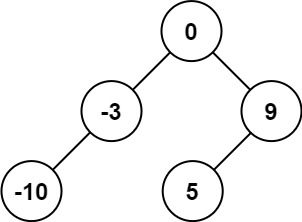
Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] is also accepted: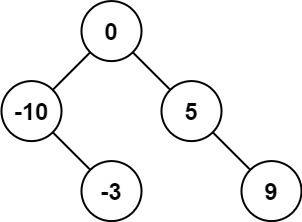

Example 2:

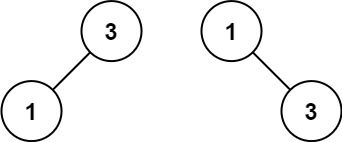
Input: nums = [1,3]
Output: [3,1]
Explanation: [1,null,3] and [3,1] are both height-balanced BSTs.

Constraints:

1 <= nums.length <= 10⁴
-10⁴ <= nums[i] <= 10⁴
nums is sorted in a strictly increasing order.

Solutions

Solution 1: Binary Search + Recursion

We design a recursive function $dfs(l, r)$, which indicates that the node values of the current binary search tree to be constructed are all within the index range $[l, r]$ of the array nums. This function returns the root node of the constructed binary search tree.

The execution process of the function $dfs(l, r)$ is as follows:

If $l > r$, it means the current array is empty, return null.
If $l \leq r$, take the element with the index $mid = \lfloor \frac{l + r}{2} \rfloor$ in the array as the root node of the current binary search tree, where $\lfloor x \rfloor$ represents rounding down $x$.
Recursively construct the left subtree of the current binary search tree, whose root node value is the element with the index $mid - 1$ in the array, and the node values of the left subtree are all within the index range $[l, mid - 1]$ of the array.
Recursively construct the right subtree of the current binary search tree, whose root node value is the element with the index $mid + 1$ in the array, and the node values of the right subtree are all within the index range $[mid + 1, r]$ of the array.
Return the root node of the current binary search tree.

The answer is the return value of the function $dfs(0, n - 1)$.

The time complexity is $O(n)$, and the space complexity is $O(\log n)$. Here, $n$ is the length of the array nums.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int[] nums;

    public TreeNode sortedArrayToBST(int[] nums) {
        this.nums = nums;
        return dfs(0, nums.length - 1);
    }

    private TreeNode dfs(int l, int r) {
        if (l > r) {
            return null;
        }
        int mid = (l + r) >> 1;
        TreeNode left = dfs(l, mid - 1);
        TreeNode right = dfs(mid + 1, r);
        return new TreeNode(nums[mid], left, right);
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        function<TreeNode*(int, int)> dfs = [&](int l, int r) -> TreeNode* {
            if (l > r) {
                return nullptr;
            }
            int mid = (l + r) >> 1;
            auto left = dfs(l, mid - 1);
            auto right = dfs(mid + 1, r);
            return new TreeNode(nums[mid], left, right);
        };
        return dfs(0, nums.size() - 1);
    }
};

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
        def dfs(l, r):
            if l > r:
                return None
            mid = (l + r) >> 1
            left = dfs(l, mid - 1)
            right = dfs(mid + 1, r)
            return TreeNode(nums[mid], left, right)

        return dfs(0, len(nums) - 1)

############

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
  def sortedArrayToBST(self, nums):
    """
    :type nums: List[int]
    :rtype: TreeNode
    """
    if nums:
      midPos = len(nums) / 2
      mid = nums[midPos]
      root = TreeNode(mid)
      root.left = self.sortedArrayToBST(nums[:midPos])
      root.right = self.sortedArrayToBST(nums[midPos + 1:])
      return root

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func sortedArrayToBST(nums []int) *TreeNode {
	var dfs func(int, int) *TreeNode
	dfs = func(l, r int) *TreeNode {
		if l > r {
			return nil
		}
		mid := (l + r) >> 1
		left, right := dfs(l, mid-1), dfs(mid+1, r)
		return &TreeNode{nums[mid], left, right}
	}
	return dfs(0, len(nums)-1)
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function sortedArrayToBST(nums: number[]): TreeNode | null {
    const n = nums.length;
    if (n === 0) {
        return null;
    }
    const mid = n >> 1;
    return new TreeNode(
        nums[mid],
        sortedArrayToBST(nums.slice(0, mid)),
        sortedArrayToBST(nums.slice(mid + 1)),
    );
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
var sortedArrayToBST = function (nums) {
    const dfs = (l, r) => {
        if (l > r) {
            return null;
        }
        const mid = (l + r) >> 1;
        const left = dfs(l, mid - 1);
        const right = dfs(mid + 1, r);
        return new TreeNode(nums[mid], left, right);
    };
    return dfs(0, nums.length - 1);
};

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    fn to_bst(nums: &Vec<i32>, start: usize, end: usize) -> Option<Rc<RefCell<TreeNode>>> {
        if start >= end {
            return None;
        }
        let mid = start + (end - start) / 2;
        Some(
            Rc::new(
                RefCell::new(TreeNode {
                    val: nums[mid],
                    left: Self::to_bst(nums, start, mid),
                    right: Self::to_bst(nums, mid + 1, end),
                })
            )
        )
    }

    pub fn sorted_array_to_bst(nums: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
        Self::to_bst(&nums, 0, nums.len())
    }
}

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    private int[] nums;

    public TreeNode SortedArrayToBST(int[] nums) {
        this.nums = nums;
        return dfs(0, nums.Length - 1);
    }

    private TreeNode dfs(int l, int r) {
        if (l > r) {
            return null;
        }
        int mid = (l + r) >> 1;
        return new TreeNode(nums[mid], dfs(l, mid - 1), dfs(mid + 1, r));
    }
}

108 - Convert Sorted Array to Binary Search Tree

108. Convert Sorted Array to Binary Search Tree

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

108. Convert Sorted Array to Binary Search Tree

Description

Solutions

All Problems

All Solutions