Question

Formatted question description: https://leetcode.ca/all/109.html

Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height-balanced binary search tree.

Example 1:

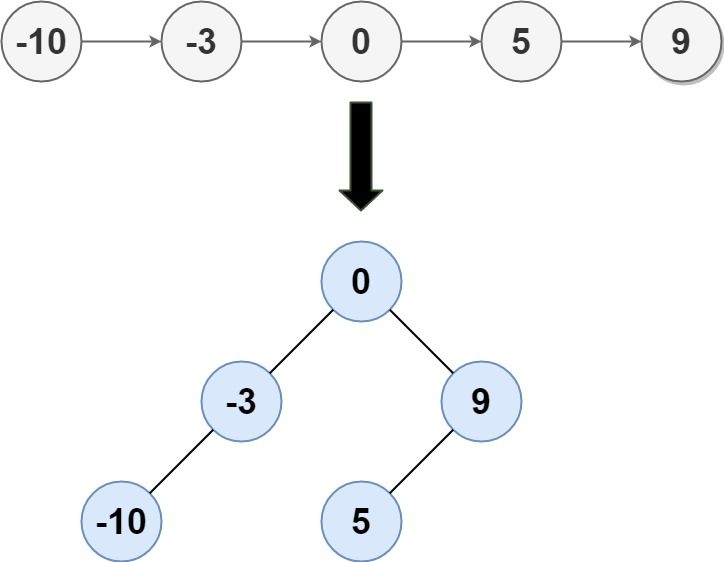
Input: head = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.

Example 2:

Input: head = []
Output: []

Constraints:

The number of nodes in head is in the range [0, 2 * 10⁴].
-10⁵ <= Node.val <= 10⁵

Algorithm

The concept applied here mirrors that of problem 108. Convert Sorted Array to Binary Search Tree, with the primary difference being the data structures involved—one utilizes an array, while the other employs a linked list.

Arrays offer the advantage of direct element access via indices, a feature not available with linked lists. This distinction becomes significant for the binary search approach, which necessitates finding the midpoint at each step.

Upon identifying the midpoint, it’s necessary to create a root node using the midpoint’s value. Subsequently, the original linked list must be divided into two separate lists, with neither including the original midpoint. These lists are then recursively processed through a depth-first search function, attaching to the root’s left and right child nodes, respectively.

Code

public class Convert_Sorted_List_to_Binary_Search_Tree {

	/**
	 * Definition for singly-linked list.
	 * public class ListNode {
	 *     int val;
	 *     ListNode next;
	 *     ListNode(int x) { val = x; next = null; }
	 * }
	 */
	/**
	 * Definition for binary tree
	 * public class TreeNode {
	 *     int val;
	 *     TreeNode left;
	 *     TreeNode right;
	 *     TreeNode(int x) { val = x; }
	 * }
	 */
    public class Solution {
        public TreeNode sortedListToBST(ListNode head) {

            if (head == null) {
                return null;
            }
            if (head.next == null) {
                return new TreeNode(head.val);
            }

            // find mid
            ListNode dummy = new ListNode(0);
            dummy.next = head;
            ListNode slow = head, fast = head, prev = dummy;
            while (fast != null && fast.next != null) {
                prev = slow;
                slow = slow.next;
                fast = fast.next.next;
            }

            // prev is one before mid
            // ListNode 2ndPartHead = slow.next; // @note@note: illegal, cannot start with number
            ListNode newHead = slow.next;
            prev.next = null; // @note: cut

            TreeNode root = new TreeNode(slow.val);
            root.left = sortedListToBST(head);
            root.right = sortedListToBST(newHead);

            return root;
        }
    }

}

############

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode sortedListToBST(ListNode head) {
        List<Integer> nums = new ArrayList<>();
        for (; head != null; head = head.next) {
            nums.add(head.val);
        }
        return buildBST(nums, 0, nums.size() - 1);
    }

    private TreeNode buildBST(List<Integer> nums, int start, int end) {
        if (start > end) {
            return null;
        }
        int mid = (start + end) >> 1;
        TreeNode root = new TreeNode(nums.get(mid));
        root.left = buildBST(nums, start, mid - 1);
        root.right = buildBST(nums, mid + 1, end);
        return root;
    }
}

// OJ: https://leetcode.com/problems/convert-sorted-list-to-binary-search-tree/
// Time: O(NlogN)
// Space: O(logN)
class Solution {
    int getLength(ListNode *head) {
        int ans = 0;
        for (; head; head = head->next, ++ans);
        return ans;
    }
    TreeNode *dfs(ListNode *head, int len) {
        if (len == 0) return NULL;
        if (len == 1) return new TreeNode(head->val);
        auto p = head;
        for (int i = 0; i < len / 2; ++i) p = p->next;
        auto root = new TreeNode(p->val);
        root->left = dfs(head, len / 2);
        root->right = dfs(p->next, (len - 1) / 2);
        return root;
    }
public:
    TreeNode* sortedListToBST(ListNode* head) {
        int len = getLength(head);
        return dfs(head, len);
    }
};

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:
        if not head:
            return None
        if not head.next:
            return TreeNode(head.val)
        
        # find mid
        dummy = ListNode(0)
        dummy.next = head
        slow, fast, prev = head, head, dummy
        while fast and fast.next:
            prev = slow
            slow = slow.next
            fast = fast.next.next
        
        # prev is one before mid
        new_head = slow.next
        prev.next = None  # cut
        
        root = TreeNode(slow.val)
        root.left = self.sortedListToBST(head)
        root.right = self.sortedListToBST(new_head)

        return root

#################

class Solution: # convert to array[], extra space => but resue method in 108
    def sortedListToBST(self, head: ListNode) -> TreeNode:
        def buildBST(nums, start, end):
            if start > end:
                return None
            mid = (start + end) >> 1
            return TreeNode(
                nums[mid], buildBST(nums, start, mid - 1), buildBST(nums, mid + 1, end)
            )

        nums = []
        while head:
            nums.append(head.val)
            head = head.next
        return buildBST(nums, 0, len(nums) - 1)

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func sortedListToBST(head *ListNode) *TreeNode {
	nums := []int{}
	for head != nil {
		nums = append(nums, head.Val)
		head = head.Next
	}
	return buildBST(nums, 0, len(nums)-1)
}

func buildBST(nums []int, start, end int) *TreeNode {
	if start > end {
		return nil
	}
	mid := (start + end) >> 1
	return &TreeNode{
		Val:   nums[mid],
		Left:  buildBST(nums, start, mid-1),
		Right: buildBST(nums, mid+1, end),
	}
}

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     val: number
 *     next: ListNode | null
 *     constructor(val?: number, next?: ListNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.next = (next===undefined ? null : next)
 *     }
 * }
 */

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

const find = (start: ListNode | null, end: ListNode | null) => {
    let fast = start;
    let slow = start;
    while (fast !== end && fast.next !== end) {
        fast = fast.next.next;
        slow = slow.next;
    }
    return slow;
};

const build = (start: ListNode | null, end: ListNode | null) => {
    if (start == end) {
        return null;
    }
    const node = find(start, end);
    return new TreeNode(node.val, build(start, node), build(node.next, end));
};

function sortedListToBST(head: ListNode | null): TreeNode | null {
    return build(head, null);
}

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {ListNode} head
 * @return {TreeNode}
 */
var sortedListToBST = function (head) {
    const buildBST = (nums, start, end) => {
        if (start > end) {
            return null;
        }
        const mid = (start + end) >> 1;
        const root = new TreeNode(nums[mid]);
        root.left = buildBST(nums, start, mid - 1);
        root.right = buildBST(nums, mid + 1, end);
        return root;
    };

    const nums = new Array();
    for (; head != null; head = head.next) {
        nums.push(head.val);
    }
    return buildBST(nums, 0, nums.length - 1);
};

// Definition for singly-linked list.
// #[derive(PartialEq, Eq, Clone, Debug)]
// pub struct ListNode {
//   pub val: i32,
//   pub next: Option<Box<ListNode>>
// }
//
// impl ListNode {
//   #[inline]
//   fn new(val: i32) -> Self {
//     ListNode {
//       next: None,
//       val
//     }
//   }
// }
// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    fn build(vals: &Vec<i32>, start: usize, end: usize) -> Option<Rc<RefCell<TreeNode>>> {
        if (start == end) {
            return None;
        }
        let mid = (start + end) >> 1;
        Some(Rc::new(RefCell::new(TreeNode {
            val: vals[mid],
            left: Self::build(vals, start, mid),
            right: Self::build(vals, mid + 1, end),
        })))
    }

    pub fn sorted_list_to_bst(head: Option<Box<ListNode>>) -> Option<Rc<RefCell<TreeNode>>> {
        let mut vals = Vec::new();
        let mut cur = &head;
        while let Some(node) = cur {
            vals.push(node.val);
            cur = &node.next;
        }
        Self::build(&vals, 0, vals.len())
    }
}

109 - Convert Sorted List to Binary Search Tree

Question

Algorithm

Code

All Problems

All Solutions

Welcome to Subscribe On Youtube

Question

Algorithm

Code

All Problems

All Solutions