Welcome to Subscribe On Youtube
106. Construct Binary Tree from Inorder and Postorder Traversal
Description
Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree.
Example 1:
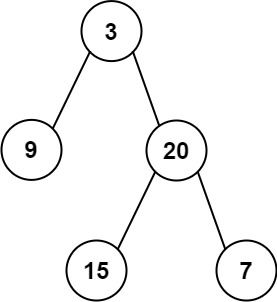
Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] Output: [3,9,20,null,null,15,7]
Example 2:
Input: inorder = [-1], postorder = [-1] Output: [-1]
Constraints:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorderandpostorderconsist of unique values.- Each value of
postorderalso appears ininorder. inorderis guaranteed to be the inorder traversal of the tree.postorderis guaranteed to be the postorder traversal of the tree.
Solutions
Solution 1: Recursion
The approach is the same as in 105. Construct Binary Tree from Preorder and Inorder Traversal.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { private Map<Integer, Integer> indexes = new HashMap<>(); public TreeNode buildTree(int[] inorder, int[] postorder) { for (int i = 0; i < inorder.length; ++i) { indexes.put(inorder[i], i); } return dfs(inorder, postorder, 0, 0, inorder.length); } private TreeNode dfs(int[] inorder, int[] postorder, int i, int j, int n) { if (n <= 0) { return null; } int v = postorder[j + n - 1]; int k = indexes.get(v); TreeNode root = new TreeNode(v); root.left = dfs(inorder, postorder, i, j, k - i); root.right = dfs(inorder, postorder, k + 1, j + k - i, n - k + i - 1); return root; } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: unordered_map<int, int> indexes; TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) { for (int i = 0; i < inorder.size(); ++i) indexes[inorder[i]] = i; return dfs(inorder, postorder, 0, 0, inorder.size()); } TreeNode* dfs(vector<int>& inorder, vector<int>& postorder, int i, int j, int n) { if (n <= 0) return nullptr; int v = postorder[j + n - 1]; int k = indexes[v]; TreeNode* root = new TreeNode(v); root->left = dfs(inorder, postorder, i, j, k - i); root->right = dfs(inorder, postorder, k + 1, j + k - i, n - k + i - 1); return root; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode: if not postorder: return None v = postorder[-1] root = TreeNode(val=v) i = inorder.index(v) root.left = self.buildTree(inorder[:i], postorder[:i]) root.right = self.buildTree(inorder[i + 1 :], postorder[i:-1]) return root ############# # Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None ''' search for index, also use .index(val) >>> a = [1,2,3,4,5] >>> a.index(3) 2 ''' class Solution(object): def buildTree(self, inorder, postorder): """ :type inorder: List[int] :type postorder: List[int] :rtype: TreeNode """ if inorder and postorder: postorder.reverse() self.index = 0 d = {} for i in range(0, len(inorder)): d[inorder[i]] = i return self.dfs(inorder, postorder, 0, len(postorder) - 1, d) def dfs(self, inorder, postorder, start, end, d): if start <= end: root = TreeNode(postorder[self.index]) mid = d[postorder[self.index]] self.index += 1 root.right = self.dfs(inorder, postorder, mid + 1, end, d) root.left = self.dfs(inorder, postorder, start, mid - 1, d) return root -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func buildTree(inorder []int, postorder []int) *TreeNode { indexes := make(map[int]int) for i, v := range inorder { indexes[v] = i } var dfs func(i, j, n int) *TreeNode dfs = func(i, j, n int) *TreeNode { if n <= 0 { return nil } v := postorder[j+n-1] k := indexes[v] root := &TreeNode{Val: v} root.Left = dfs(i, j, k-i) root.Right = dfs(k+1, j+k-i, n-k+i-1) return root } return dfs(0, 0, len(inorder)) } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function buildTree(inorder: number[], postorder: number[]): TreeNode | null { const n = postorder.length; if (n == 0) { return null; } const val = postorder[n - 1]; const index = inorder.indexOf(val); return new TreeNode( val, buildTree(inorder.slice(0, index), postorder.slice(0, index)), buildTree(inorder.slice(index + 1), postorder.slice(index, n - 1)), ); } -
// Definition for a binary tree node. // #[derive(Debug, PartialEq, Eq)] // pub struct TreeNode { // pub val: i32, // pub left: Option<Rc<RefCell<TreeNode>>>, // pub right: Option<Rc<RefCell<TreeNode>>>, // } // // impl TreeNode { // #[inline] // pub fn new(val: i32) -> Self { // TreeNode { // val, // left: None, // right: None // } // } // } use std::rc::Rc; use std::cell::RefCell; impl Solution { fn reset( inorder: &Vec<i32>, i_left: usize, i_right: usize, postorder: &Vec<i32>, p_left: usize, p_right: usize ) -> Option<Rc<RefCell<TreeNode>>> { if i_left == i_right { return None; } let val = postorder[p_right - 1]; let index = inorder .iter() .position(|&v| v == val) .unwrap(); Some( Rc::new( RefCell::new(TreeNode { val, left: Self::reset( inorder, i_left, index, postorder, p_left, p_left + index - i_left ), right: Self::reset( inorder, index + 1, i_right, postorder, p_left + index - i_left, p_right - 1 ), }) ) ) } pub fn build_tree(inorder: Vec<i32>, postorder: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> { let n = inorder.len(); Self::reset(&inorder, 0, n, &postorder, 0, n) } }