Welcome to Subscribe On Youtube
101. Symmetric Tree
Description
Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).
Example 1:
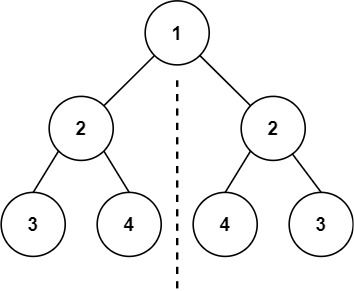
Input: root = [1,2,2,3,4,4,3] Output: true
Example 2:
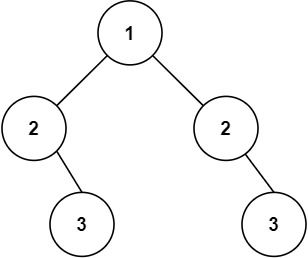
Input: root = [1,2,2,null,3,null,3] Output: false
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. -100 <= Node.val <= 100
Follow up: Could you solve it both recursively and iteratively?
Solutions
Solution 1: Recursion
We design a function $dfs(root1, root2)$ to determine whether two binary trees are symmetric. The answer is $dfs(root, root)$.
The logic of the function $dfs(root1, root2)$ is as follows:
- If both $root1$ and $root2$ are null, then the two binary trees are symmetric, return
true. - If only one of $root1$ and $root2$ is null, or if $root1.val \neq root2.val$, then the two binary trees are not symmetric, return
false. - Otherwise, determine whether the left subtree of $root1$ is symmetric to the right subtree of $root2$, and whether the right subtree of $root1$ is symmetric to the left subtree of $root2$. Here we use recursion.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public boolean isSymmetric(TreeNode root) { return dfs(root, root); } private boolean dfs(TreeNode root1, TreeNode root2) { if (root1 == null && root2 == null) { return true; } if (root1 == null || root2 == null || root1.val != root2.val) { return false; } return dfs(root1.left, root2.right) && dfs(root1.right, root2.left); } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: bool isSymmetric(TreeNode* root) { function<bool(TreeNode*, TreeNode*)> dfs = [&](TreeNode* root1, TreeNode* root2) -> bool { if (!root1 && !root2) return true; if (!root1 || !root2 || root1->val != root2->val) return false; return dfs(root1->left, root2->right) && dfs(root1->right, root2->left); }; return dfs(root, root); } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isSymmetric(self, root: Optional[TreeNode]) -> bool: def dfs(root1, root2): if root1 is None and root2 is None: return True if root1 is None or root2 is None or root1.val != root2.val: return False return dfs(root1.left, root2.right) and dfs(root1.right, root2.left) return dfs(root, root) -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func isSymmetric(root *TreeNode) bool { var dfs func(*TreeNode, *TreeNode) bool dfs = func(root1, root2 *TreeNode) bool { if root1 == nil && root2 == nil { return true } if root1 == nil || root2 == nil || root1.Val != root2.Val { return false } return dfs(root1.Left, root2.Right) && dfs(root1.Right, root2.Left) } return dfs(root, root) } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ const dfs = (root1: TreeNode | null, root2: TreeNode | null) => { if (root1 == root2) { return true; } if (root1 == null || root2 == null || root1.val != root2.val) { return false; } return dfs(root1.left, root2.right) && dfs(root1.right, root2.left); }; function isSymmetric(root: TreeNode | null): boolean { return dfs(root.left, root.right); } -
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {boolean} */ var isSymmetric = function (root) { function dfs(root1, root2) { if (!root1 && !root2) return true; if (!root1 || !root2 || root1.val != root2.val) return false; return dfs(root1.left, root2.right) && dfs(root1.right, root2.left); } return dfs(root, root); }; -
// Definition for a binary tree node. // #[derive(Debug, PartialEq, Eq)] // pub struct TreeNode { // pub val: i32, // pub left: Option<Rc<RefCell<TreeNode>>>, // pub right: Option<Rc<RefCell<TreeNode>>>, // } // // impl TreeNode { // #[inline] // pub fn new(val: i32) -> Self { // TreeNode { // val, // left: None, // right: None // } // } // } use std::rc::Rc; use std::cell::RefCell; impl Solution { fn dfs(root1: &Option<Rc<RefCell<TreeNode>>>, root2: &Option<Rc<RefCell<TreeNode>>>) -> bool { if root1.is_none() && root2.is_none() { return true; } if root1.is_none() || root2.is_none() { return false; } let node1 = root1.as_ref().unwrap().borrow(); let node2 = root2.as_ref().unwrap().borrow(); node1.val == node2.val && Self::dfs(&node1.left, &node2.right) && Self::dfs(&node1.right, &node2.left) } pub fn is_symmetric(root: Option<Rc<RefCell<TreeNode>>>) -> bool { let node = root.as_ref().unwrap().borrow(); Self::dfs(&node.left, &node.right) } }