Welcome to Subscribe On Youtube
98. Validate Binary Search Tree
Description
Given the root of a binary tree, determine if it is a valid binary search tree (BST).
A valid BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
Example 1:
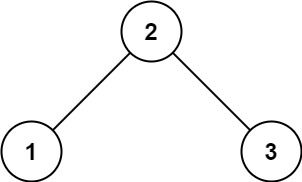
Input: root = [2,1,3] Output: true
Example 2:
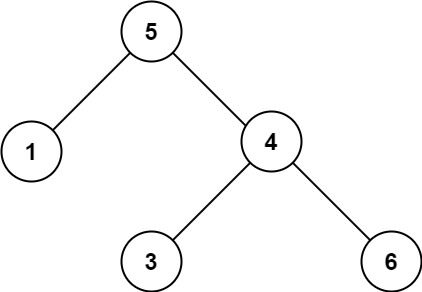
Input: root = [5,1,4,null,null,3,6] Output: false Explanation: The root node's value is 5 but its right child's value is 4.
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. -231 <= Node.val <= 231 - 1
Solutions
Solution 1: Recursion
In-order traversal. If it is a valid binary search tree, then the sequence traversed should be monotonically increasing. So, we only need to compare and judge whether the current number traversed is greater than the previous number.
Alternatively, consider the subtree with root as the root, whether all node values are within the valid range, and judge recursively.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the tree.
Note: remember below in invalid, 7 should go right of 5
5
/ \
1 8
\ \
7 10
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { private Integer prev; public boolean isValidBST(TreeNode root) { prev = null; return dfs(root); } private boolean dfs(TreeNode root) { if (root == null) { return true; } if (!dfs(root.left)) { return false; } if (prev != null && prev >= root.val) { return false; } prev = root.val; if (!dfs(root.right)) { return false; } return true; } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: TreeNode* prev; bool isValidBST(TreeNode* root) { prev = nullptr; return dfs(root); } bool dfs(TreeNode* root) { if (!root) return true; if (!dfs(root->left)) return false; if (prev && prev->val >= root->val) return false; prev = root; if (!dfs(root->right)) return false; return true; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right # Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: # recursive def isValidBST(self, root: Optional[TreeNode]) -> bool: def dfs(root, mi, ma): if not root: return True return mi < root.val < ma and dfs(root.left, mi, root.val) and dfs(root.right, root.val, ma) return dfs(root, -math.inf, math.inf) class Solution: # iterative def isValidBST(self, root: TreeNode) -> bool: # store (node, lower, upper) tuples in a single queue queue = [(root, None, None)] # another option: # queue = [(root, -math.inf, math.inf)] while queue: node, lower, upper = queue.pop(0) if node is None: continue val = node.val if lower is not None and val <= lower: return False if upper is not None and val >= upper: return False queue.append((node.right, val, upper)) queue.append((node.left, lower, val)) return True ############ class Solution: def isValidBST(self, root: Optional[TreeNode]) -> bool: def isValidBST(root: Optional[TreeNode], minNode: Optional[TreeNode], maxNode: Optional[TreeNode]) -> bool: if not root: return True if minNode and root.val <= minNode.val: return False if maxNode and root.val >= maxNode.val: return False return isValidBST(root.left, minNode, root) and isValidBST(root.right, root, maxNode) return isValidBST(root, None, None) ############ # Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isValidBST(self, root: TreeNode) -> bool: def dfs(root): nonlocal prev if root is None: return True if not dfs(root.left): return False if prev >= root.val: return False prev = root.val if not dfs(root.right): return False return True prev = -inf return dfs(root) ############ # Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution(object): def isValidBST(self, root): """ :type root: TreeNode :rtype: bool """ prev = -float("inf") stack = [(1, root)] while stack: p = stack.pop() if not p[1]: continue if p[0] == 0: if p[1].val <= prev: return False prev = p[1].val else: stack.append((1, p[1].right)) stack.append((0, p[1])) stack.append((1, p[1].left)) return True -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func isValidBST(root *TreeNode) bool { var prev *TreeNode var dfs func(root *TreeNode) bool dfs = func(root *TreeNode) bool { if root == nil { return true } if !dfs(root.Left) { return false } if prev != nil && prev.Val >= root.Val { return false } prev = root if !dfs(root.Right) { return false } return true } return dfs(root) } -
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {boolean} */ var isValidBST = function (root) { let prev = null; let dfs = function (root) { if (!root) { return true; } if (!dfs(root.left)) { return false; } if (prev && prev.val >= root.val) { return false; } prev = root; if (!dfs(root.right)) { return false; } return true; }; return dfs(root); }; -
/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { private TreeNode prev; public bool IsValidBST(TreeNode root) { prev = null; return dfs(root); } private bool dfs(TreeNode root) { if (root == null) { return true; } if (!dfs(root.left)) { return false; } if (prev != null && prev.val >= root.val) { return false; } prev = root; if (!dfs(root.right)) { return false; } return true; } } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function isValidBST(root: TreeNode | null): boolean { let prev: TreeNode | null = null; const dfs = (root: TreeNode | null): boolean => { if (!root) { return true; } if (!dfs(root.left)) { return false; } if (prev && prev.val >= root.val) { return false; } prev = root; return dfs(root.right); }; return dfs(root); } -
// Definition for a binary tree node. // #[derive(Debug, PartialEq, Eq)] // pub struct TreeNode { // pub val: i32, // pub left: Option<Rc<RefCell<TreeNode>>>, // pub right: Option<Rc<RefCell<TreeNode>>>, // } // // impl TreeNode { // #[inline] // pub fn new(val: i32) -> Self { // TreeNode { // val, // left: None, // right: None // } // } // } use std::rc::Rc; use std::cell::RefCell; impl Solution { fn dfs(root: &Option<Rc<RefCell<TreeNode>>>, prev: &mut Option<i32>) -> bool { if root.is_none() { return true; } let root = root.as_ref().unwrap().borrow(); if !Self::dfs(&root.left, prev) { return false; } if prev.is_some() && prev.unwrap() >= root.val { return false; } *prev = Some(root.val); Self::dfs(&root.right, prev) } pub fn is_valid_bst(root: Option<Rc<RefCell<TreeNode>>>) -> bool { Self::dfs(&root, &mut None) } }