Welcome to Subscribe On Youtube
99. Recover Binary Search Tree
Description
You are given the root of a binary search tree (BST), where the values of exactly two nodes of the tree were swapped by mistake. Recover the tree without changing its structure.
Example 1:
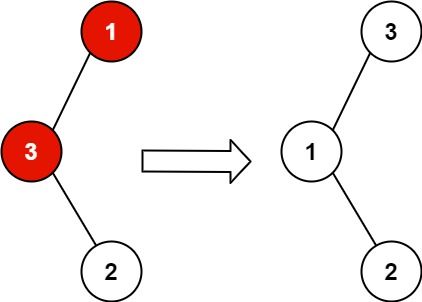
Input: root = [1,3,null,null,2] Output: [3,1,null,null,2] Explanation: 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.
Example 2:
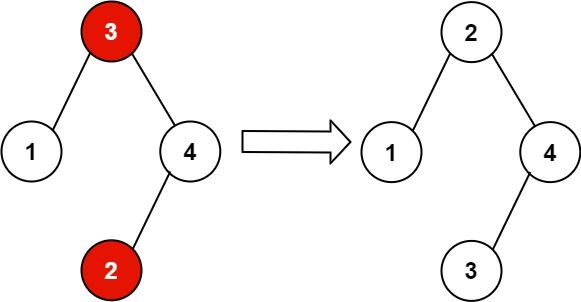
Input: root = [3,1,4,null,null,2] Output: [2,1,4,null,null,3] Explanation: 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.
Constraints:
- The number of nodes in the tree is in the range
[2, 1000]. -231 <= Node.val <= 231 - 1
Follow up: A solution using O(n) space is pretty straight-forward. Could you devise a constant O(1) space solution?
Solutions
Solution 1: In-order Traversal
In-order traversal of a binary search tree results in an increasing sequence. If two nodes’ values are mistakenly swapped, there will definitely be two reverse pairs in the sequence obtained from the in-order traversal. We use first and second to record the smaller and larger values of these two reverse pairs, respectively. Finally, swapping the values of these two nodes will correct the mistake.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary search tree.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { private TreeNode prev; private TreeNode first; private TreeNode second; public void recoverTree(TreeNode root) { dfs(root); int t = first.val; first.val = second.val; second.val = t; } private void dfs(TreeNode root) { if (root == null) { return; } dfs(root.left); if (prev != null && prev.val > root.val) { if (first == null) { first = prev; } second = root; } prev = root; dfs(root.right); } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: void recoverTree(TreeNode* root) { TreeNode* prev = nullptr; TreeNode* first = nullptr; TreeNode* second = nullptr; function<void(TreeNode * root)> dfs = [&](TreeNode* root) { if (!root) return; dfs(root->left); if (prev && prev->val > root->val) { if (!first) first = prev; second = root; } prev = root; dfs(root->right); }; dfs(root); swap(first->val, second->val); } }; -
''' Without nonlocal, any assignment to prev, first, and second inside dfs would be treated as creating new local variables within dfs, rather than modifying the outer variables. ''' # Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def recoverTree(self, root: Optional[TreeNode]) -> None: """ Do not return anything, modify root in-place instead. """ def dfs(root): if root is None: return nonlocal prev, first, second dfs(root.left) if prev and prev.val > root.val: if first is None: first = prev second = root prev = root dfs(root.right) prev = first = second = None dfs(root) first.val, second.val = second.val, first.val -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func recoverTree(root *TreeNode) { var prev, first, second *TreeNode var dfs func(*TreeNode) dfs = func(root *TreeNode) { if root == nil { return } dfs(root.Left) if prev != nil && prev.Val > root.Val { if first == nil { first = prev } second = root } prev = root dfs(root.Right) } dfs(root) first.Val, second.Val = second.Val, first.Val } -
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {void} Do not return anything, modify root in-place instead. */ var recoverTree = function (root) { let prev = null; let first = null; let second = null; function dfs(root) { if (!root) { return; } dfs(root.left); if (prev && prev.val > root.val) { if (!first) { first = prev; } second = root; } prev = root; dfs(root.right); } dfs(root); const t = first.val; first.val = second.val; second.val = t; }; -
/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { private TreeNode prev, first, second; public void RecoverTree(TreeNode root) { dfs(root); int t = first.val; first.val = second.val; second.val = t; } private void dfs(TreeNode root) { if (root == null) { return; } dfs(root.left); if (prev != null && prev.val > root.val) { if (first == null) { first = prev; } second = root; } prev = root; dfs(root.right); } }