Welcome to Subscribe On Youtube
96. Unique Binary Search Trees
Description
Given an integer n, return the number of structurally unique BST's (binary search trees) which has exactly n nodes of unique values from 1 to n.
Example 1:
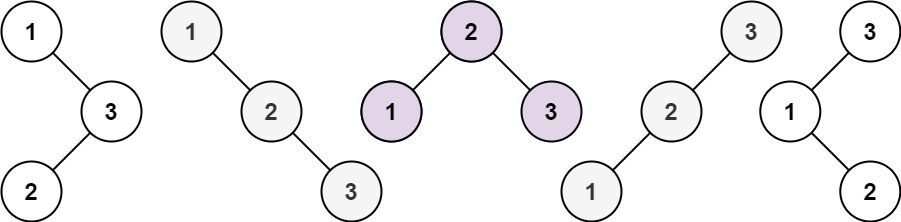
Input: n = 3 Output: 5
Example 2:
Input: n = 1 Output: 1
Constraints:
1 <= n <= 19
Solutions
Solution 1: Dynamic Programming
We define $f[i]$ to represent the number of binary search trees that can be generated from $[1, i]$. Initially, $f[0] = 1$, and the answer is $f[n]$.
We can enumerate the number of nodes $i$, then the number of nodes in the left subtree $j \in [0, i - 1]$, and the number of nodes in the right subtree $k = i - j - 1$. The number of combinations of the number of nodes in the left subtree and the right subtree is $f[j] \times f[k]$, so $f[i] = \sum_{j = 0}^{i - 1} f[j] \times f[i - j - 1]$.
Finally, return $f[n]$.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes.
Let’s first look at the situation when n = 1, only a single binary search tree can be formed. The situations where n is 1, 2, and 3 are as follows:
1 n = 1
2 1 n = 2
/ \
1 2
1 3 3 2 1 n = 3
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
We assign 1 when n = 0, because the empty tree is also a binary search tree, then the situation when n = 1 can be regarded as the number of left subtrees multiplied by the number of right subtrees, and the left and right subtrees Trees are all empty trees, so 1 by 1 is still 1. Then when n = 2, since both 1 and 2 can be roots, you can calculate them separately and add them together. The case of n = 2 can be calculated by the following formula (where dp[i] represents the number of BST that can be composed of i numbers):
dp[2] =
dp[0] * dp[1]
(If 1 is the root, the left subtree must not exist, and the right subtree can have a number)
+
dp[1] * dp[0]
(If 2 is the root, the left subtree can have a number, and the right subtree must not exist)
In the same way, the calculation method for n = 3 can be written:
dp[3] =
dp[0] * dp[2]
(If 1 is the root, the left subtree must not exist, and the right subtree can have two numbers)
+
dp[1] * dp[1]
(If 2 is the root, the left and right subtrees can each have a number)
+
dp[2] * dp[0]
(If 3 is the root, the left subtree can have two numbers, and the right subtree must not exist)
-
public class Unique_Binary_Search_Trees { public static void main(String[] args) { Unique_Binary_Search_Trees out = new Unique_Binary_Search_Trees(); Solution s = out.new Solution(); System.out.println(s.numTrees(3)); } public class Solution { public int numTrees(int n) { if (n <= 0) { return 0; } // dp[i] represents the number of BST that can be composed of i numbers int[] dp = new int[n + 1]; dp[0] = 1; // null is counted as one unique tree for (int i = 1; i <= n; i++) { // 1...n for (int j = 1; j <= i; j++) { // for each fixed n, calculate its sum dp[i] += dp[j - 1] * dp[i - j]; } } return dp[n]; } } public class Solution_recursion { public int numTrees(int n) { if (n < 0) { return 0; } if (n == 0 || n == 1) { return 1; } int sum = 0; for (int i = 1; i <= n; i++) { // 2 conditions: unique && BST. => inorder-visit will generate ordered sequence // so, if decide root, then left and right can be calculated // @note: root is "i", left has "i-1" nodes, right has "n - (i - 1) - 1"=="n - i" nodes sum += numTrees(i - 1) * numTrees(n - i); } return sum; } } } ////// class Solution { public int numTrees(int n) { int[] dp = new int[n + 1]; dp[0] = 1; for (int i = 1; i <= n; ++i) { for (int j = 0; j < i; ++j) { dp[i] += dp[j] * dp[i - j - 1]; } } return dp[n]; } } -
class Solution { public: int numTrees(int n) { vector<int> f(n + 1); f[0] = 1; for (int i = 1; i <= n; ++i) { for (int j = 0; j < i; ++j) { f[i] += f[j] * f[i - j - 1]; } } return f[n]; } }; -
class Solution: def numTrees(self, n: int) -> int: dp = [0] * (n + 1) dp[0] = 1 # e.g, null is counted as one unique tree for i in range(1, n + 1): # up to i-1, when j=i-1 meaning left child having i-1 node then i is the root for j in range(i): dp[i] += dp[j] * dp[i - j - 1] # -1, not counting root return dp[-1] ############ class Solution(object): def _numTrees(self, n): """ :type n: int :rtype: int """ dp = [0] * (n + 1) dp[0] = dp[1] = 1 for i in range(2, n + 1): for j in range(1, i + 1): dp[i] += dp[j - 1] * dp[i - j] return dp[-1] def numTrees(self, n): ans = 1 for i in range(1, n + 1): ans = ans * (n + i) / i return ans / (n + 1) -
func numTrees(n int) int { f := make([]int, n+1) f[0] = 1 for i := 1; i <= n; i++ { for j := 0; j < i; j++ { f[i] += f[j] * f[i-j-1] } } return f[n] } -
function numTrees(n: number): number { const f: number[] = Array(n + 1).fill(0); f[0] = 1; for (let i = 1; i <= n; ++i) { for (let j = 0; j < i; ++j) { f[i] += f[j] * f[i - j - 1]; } } return f[n]; } -
public class Solution { public int NumTrees(int n) { int[] f = new int[n + 1]; f[0] = 1; for (int i = 1; i <= n; ++i) { for (int j = 0; j < i; ++j) { f[i] += f[j] * f[i - j - 1]; } } return f[n]; } } -
impl Solution { pub fn num_trees(n: i32) -> i32 { let n = n as usize; let mut f = vec![0; n + 1]; f[0] = 1; for i in 1..=n { for j in 0..i { f[i] += f[j] * f[i - j - 1]; } } f[n] as i32 } }