Welcome to Subscribe On Youtube
95. Unique Binary Search Trees II
Description
Given an integer n, return all the structurally unique BST's (binary search trees), which has exactly n nodes of unique values from 1 to n. Return the answer in any order.
Example 1:
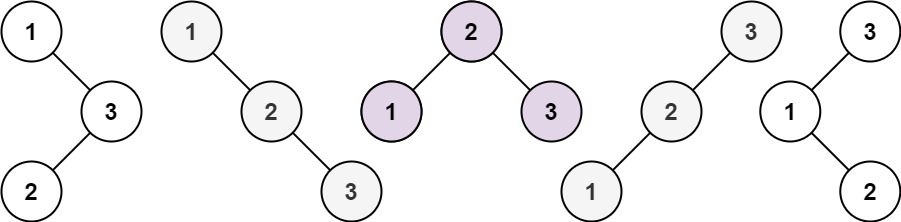
Input: n = 3 Output: [[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
Example 2:
Input: n = 1 Output: [[1]]
Constraints:
1 <= n <= 8
Solutions
Solution 1: DFS (Depth-First Search)
We design a function $dfs(i, j)$ that returns all feasible binary search trees composed of $[i, j]$, so the answer is $dfs(1, n)$.
The execution steps of the function $dfs(i, j)$ are as follows:
- If $i > j$, it means that there are no numbers to form a binary search tree at this time, so return a list consisting of a null node.
- If $i \leq j$, we enumerate the numbers $v$ in $[i, j]$ as the root node. The left subtree of the root node $v$ is composed of $[i, v - 1]$, and the right subtree is composed of $[v + 1, j]$. Finally, we take the Cartesian product of all combinations of the left and right subtrees, i.e., $left \times right$, add the root node $v$, and get all binary search trees with $v$ as the root node.
The time complexity is $O(n \times G(n))$, and the space complexity is $O(n \times G(n))$. Where $G(n)$ is the Catalan number.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public List<TreeNode> generateTrees(int n) { return dfs(1, n); } private List<TreeNode> dfs(int i, int j) { List<TreeNode> ans = new ArrayList<>(); if (i > j) { ans.add(null); return ans; } for (int v = i; v <= j; ++v) { var left = dfs(i, v - 1); var right = dfs(v + 1, j); for (var l : left) { for (var r : right) { ans.add(new TreeNode(v, l, r)); } } } return ans; } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: vector<TreeNode*> generateTrees(int n) { function<vector<TreeNode*>(int, int)> dfs = [&](int i, int j) { if (i > j) { return vector<TreeNode*>{nullptr}; } vector<TreeNode*> ans; for (int v = i; v <= j; ++v) { auto left = dfs(i, v - 1); auto right = dfs(v + 1, j); for (auto l : left) { for (auto r : right) { ans.push_back(new TreeNode(v, l, r)); } } } return ans; }; return dfs(1, n); } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def generateTrees(self, n: int) -> List[TreeNode]: def gen(left, right): ans = [] # this if check instead of if left==right then return Node(left), less hassle if left > right: ans.append(None) else: # right+1, to cover case when left==right for i in range(left, right + 1): left_trees = gen(left, i - 1) right_trees = gen(i + 1, right) for l in left_trees: for r in right_trees: node = TreeNode(i, l, r) ans.append(node) return ans return gen(1, n) # n or right is inclusive ############ # Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def generateTrees(self, n: int) -> List[Optional[TreeNode]]: def dfs(i: int, j: int) -> List[Optional[TreeNode]]: if i > j: return [None] ans = [] for v in range(i, j + 1): left = dfs(i, v - 1) right = dfs(v + 1, j) for l in left: for r in right: ans.append(TreeNode(v, l, r)) return ans return dfs(1, n) -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func generateTrees(n int) []*TreeNode { var dfs func(int, int) []*TreeNode dfs = func(i, j int) []*TreeNode { if i > j { return []*TreeNode{nil} } ans := []*TreeNode{} for v := i; v <= j; v++ { left := dfs(i, v-1) right := dfs(v+1, j) for _, l := range left { for _, r := range right { ans = append(ans, &TreeNode{v, l, r}) } } } return ans } return dfs(1, n) } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function generateTrees(n: number): Array<TreeNode | null> { const dfs = (i: number, j: number): Array<TreeNode | null> => { if (i > j) { return [null]; } const ans: Array<TreeNode | null> = []; for (let v = i; v <= j; ++v) { const left = dfs(i, v - 1); const right = dfs(v + 1, j); for (const l of left) { for (const r of right) { ans.push(new TreeNode(v, l, r)); } } } return ans; }; return dfs(1, n); } -
// Definition for a binary tree node. // #[derive(Debug, PartialEq, Eq)] // pub struct TreeNode { // pub val: i32, // pub left: Option<Rc<RefCell<TreeNode>>>, // pub right: Option<Rc<RefCell<TreeNode>>>, // } // // impl TreeNode { // #[inline] // pub fn new(val: i32) -> Self { // TreeNode { // val, // left: None, // right: None // } // } // } use std::rc::Rc; use std::cell::RefCell; impl Solution { pub fn generate_trees(n: i32) -> Vec<Option<Rc<RefCell<TreeNode>>>> { Self::dfs(1, n) } fn dfs(i: i32, j: i32) -> Vec<Option<Rc<RefCell<TreeNode>>>> { let mut ans = Vec::new(); if i > j { ans.push(None); return ans; } for v in i..=j { let left = Self::dfs(i, v - 1); let right = Self::dfs(v + 1, j); for l in &left { for r in &right { ans.push( Some( Rc::new( RefCell::new(TreeNode { val: v, left: l.clone(), right: r.clone(), }) ) ) ); } } } ans } }