Welcome to Subscribe On Youtube
94. Binary Tree Inorder Traversal
Description
Given the root of a binary tree, return the inorder traversal of its nodes' values.
Example 1:
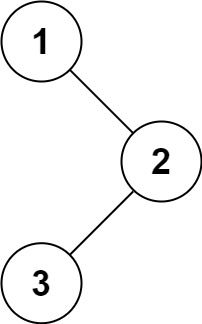
Input: root = [1,null,2,3] Output: [1,3,2]
Example 2:
Input: root = [] Output: []
Example 3:
Input: root = [1] Output: [1]
Constraints:
- The number of nodes in the tree is in the range
[0, 100]. -100 <= Node.val <= 100
Follow up: Recursive solution is trivial, could you do it iteratively?
Solutions
Solution 1: Recursive Traversal
We first recursively traverse the left subtree, then visit the root node, and finally recursively traverse the right subtree.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree, and the space complexity mainly depends on the stack space of the recursive call.
Solution 2: Stack Implementation for Non-recursive Traversal
The non-recursive approach is as follows:
- Define a stack
stk. - Push the left nodes of the tree into the stack in sequence.
- When the left node is null, pop and process the top element of the stack.
- Repeat steps 2-3.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree, and the space complexity mainly depends on the stack space.
Solution 3: Morris Implementation for In-order Traversal
Morris traversal does not require a stack, so the space complexity is $O(1)$. The core idea is:
Traverse the binary tree nodes,
- If the left subtree of the current node
rootis null, add the current node value to the result listans, and update the current node toroot.right. - If the left subtree of the current node
rootis not null, find the rightmost nodeprevof the left subtree (which is the predecessor node of therootnode in in-order traversal):- If the right subtree of the predecessor node
previs null, point the right subtree of the predecessor node to the current noderoot, and update the current node toroot.left. - If the right subtree of the predecessor node
previs not null, add the current node value to the result listans, then point the right subtree of the predecessor node to null (i.e., disconnectprevandroot), and update the current node toroot.right.
- If the right subtree of the predecessor node
- Repeat the above steps until the binary tree node is null, and the traversal ends.
The time complexity is $O(n)$, and the space complexity is $O(1)$. Here, $n$ is the number of nodes in the binary tree.
-
import java.util.ArrayList; import java.util.HashSet; import java.util.List; import java.util.Stack; public class Binary_Tree_Inorder_Traversal { /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ public class Solution_optmize { public List<Integer> inorderTraversal(TreeNode root) { List<Integer> list = new ArrayList<Integer>(); if (root == null) { return list; } Stack<TreeNode> sk = new Stack<>(); TreeNode current = root; while (!sk.isEmpty() || current != null) { while (current != null) { sk.push(current); current = current.left; } // @note: 一逼撸到最左边 // @note: 没有push left的操作,就不会无限循环,也不需要mark是否visited TreeNode leftOrMiddle = sk.pop(); list.add(leftOrMiddle.val); current = leftOrMiddle.right; // if right is null here, next time pop parent node } return list; } } class Solution_noStack { // but modifying original tree public List<Integer> inorderTraversal(TreeNode root) { List<Integer> result = new ArrayList<>(); TreeNode current = root; TreeNode prev; while (current != null) { if (current.left == null) { result.add(current.val); // only handle right child current = current.right; // move to next right node } else { // has a left subtree prev = current.left; while (prev.right != null) { // find rightmost prev = prev.right; } prev.right = current; // put cur after the pre node TreeNode temp = current; // store cur node current = current.left; // move cur to the top of the new tree temp.left = null; // original cur left be null, avoid infinite loops } } return result; } } public class Solution { List<Integer> list = new ArrayList<Integer>(); public List<Integer> inorderTraversal(TreeNode root) { // mark if a node is visited already: true is visited. or, just use a Set HashSet<TreeNode> hs = new HashSet<>(); Stack<TreeNode> sk = new Stack<>(); sk.push(root); while (!sk.isEmpty()) { TreeNode current = sk.pop(); if (current == null) { continue; } // @note: careful to check left visited, or else infinite looping if (current.left != null && !hs.contains(current.left)) { sk.push(current); sk.push(current.left); } else { if (current.right != null && !hs.contains(current.right)) { sk.push(current.right); } hs.add(current); list.add(current.val); } } return list; } } class Solution_recursion { List<Integer> result = new ArrayList<>(); public List<Integer> inorderTraversal(TreeNode root) { dfs(root); return result; } public void dfs(TreeNode root) { if (root == null) { return; } dfs(root.left); result.add(root.val); dfs(root.right); } } } ////// /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public List<Integer> inorderTraversal(TreeNode root) { List<Integer> ans = new ArrayList<>(); while (root != null) { if (root.left == null) { ans.add(root.val); root = root.right; } else { TreeNode prev = root.left; while (prev.right != null && prev.right != root) { prev = prev.right; } if (prev.right == null) { prev.right = root; root = root.left; } else { ans.add(root.val); prev.right = null; root = root.right; } } } return ans; } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: vector<int> inorderTraversal(TreeNode* root) { vector<int> ans; while (root) { if (!root->left) { ans.push_back(root->val); root = root->right; } else { TreeNode* prev = root->left; while (prev->right && prev->right != root) { prev = prev->right; } if (!prev->right) { prev->right = root; root = root->left; } else { ans.push_back(root->val); prev->right = nullptr; root = root->right; } } } return ans; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]: stack = [] current = root res = [] while stack or current: while current: stack.append(current) current = current.left left_or_middle = stack.pop() res.append(left_or_middle.val) current = left_or_middle.right return res # no stack, but modifying original tree class Solution: def inorderTraversal(self, root): result = [] current = root prev = None while current: if current.left is None: result.append(current.val) current = current.right else: prev = current.left while prev.right: prev = prev.right prev.right = current temp = current current = current.left temp.left = None return result class Solution: def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]: ans = [] while root: if root.left is None: ans.append(root.val) root = root.right else: prev = root.left while prev.right and prev.right != root: prev = prev.right if prev.right is None: prev.right = root root = root.left else: ans.append(root.val) prev.right = None root = root.right return ans ########### # Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None ''' >>> stack = [(1, None)] >>> stack.extend([(0, None), (2, "b"), (3, "c")]) >>> stack [(1, None), (0, None), (2, 'b'), (3, 'c')] ''' class Solution(object): def inorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ # stack to hold tuple (), '0' meaning a parent node for current level, '1' meaning a child node res, stack = [], [(1, root)] while stack: p = stack.pop() if not p[1]: continue stack.extend([(1, p[1].right), (0, p[1]), (1, p[1].left)]) if p[0] != 0 else res.append(p[1].val) return res -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func inorderTraversal(root *TreeNode) []int { var ans []int for root != nil { if root.Left == nil { ans = append(ans, root.Val) root = root.Right } else { prev := root.Left for prev.Right != nil && prev.Right != root { prev = prev.Right } if prev.Right == nil { prev.Right = root root = root.Left } else { ans = append(ans, root.Val) prev.Right = nil root = root.Right } } } return ans } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function inorderTraversal(root: TreeNode | null): number[] { if (root == null) { return []; } return [...inorderTraversal(root.left), root.val, ...inorderTraversal(root.right)]; } -
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number[]} */ var inorderTraversal = function (root) { let ans = []; while (root) { if (!root.left) { ans.push(root.val); root = root.right; } else { let prev = root.left; while (prev.right && prev.right != root) { prev = prev.right; } if (!prev.right) { prev.right = root; root = root.left; } else { ans.push(root.val); prev.right = null; root = root.right; } } } return ans; }; -
// Definition for a binary tree node. // #[derive(Debug, PartialEq, Eq)] // pub struct TreeNode { // pub val: i32, // pub left: Option<Rc<RefCell<TreeNode>>>, // pub right: Option<Rc<RefCell<TreeNode>>>, // } // // impl TreeNode { // #[inline] // pub fn new(val: i32) -> Self { // TreeNode { // val, // left: None, // right: None // } // } // } use std::rc::Rc; use std::cell::RefCell; impl Solution { fn dfs(root: &Option<Rc<RefCell<TreeNode>>>, res: &mut Vec<i32>) { if root.is_none() { return; } let node = root.as_ref().unwrap().borrow(); Self::dfs(&node.left, res); res.push(node.val); Self::dfs(&node.right, res); } pub fn inorder_traversal(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> { let mut res = vec![]; Self::dfs(&root, &mut res); res } }