Question

Formatted question description: https://leetcode.ca/all/85.html

Given a rows x cols binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.

Example 1:

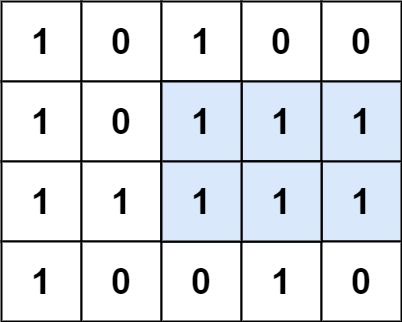
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 6
Explanation: The maximal rectangle is shown in the above picture.

Example 2:

Input: matrix = [["0"]]
Output: 0

Example 3:

Input: matrix = [["1"]]
Output: 1

Constraints:

rows == matrix.length
cols == matrix[i].length
1 <= row, cols <= 200
matrix[i][j] is '0' or '1'.

Algorithm

This question is an extension of the previous 84. Largest Rectangle in Histogram https://leetcode.ca/2016-02-22-84-Largest-Rectangle-in-Histogram/. The two-dimensional matrix of this question can be seen as a histogram at each level upwards.

For each histogram to call the method in 84. Largest Rectangle in Histogram https://leetcode.ca/2016-02-22-84-Largest-Rectangle-in-Histogram/ to get the largest rectangle area.

The primary task in this question is to approach each layer as if it were the base layer of a histogram and then build the histogram upwards from there. Given that the input matrix is constrained to contain only the characters ‘0’ and ‘1’, processing it becomes comparatively straightforward. The approach involves, for each element, assigning a value of 0 if the element is ‘0’, or if the element is ‘1’, assigning a value that is one more than the height value of the previous layer.

Code

import java.util.Arrays;
import java.util.Stack;

public class Solution {
        public int maximalRectangle(char[][] m) {
            /*
	        original:

	        "0010",
	        "1111",
	        "1111",
	        "0111",
	        "1100",
	        "1111",
	        "1110"

	        */



		/*
			"01101",
			"11010",
			"01110",
			"11110",
			"11111",
			"00000",


			[0, 1, 1, 0, 1],
			[1, 2, 0, 1, 0],
			[0, 3, 1, 2, 0],
			[1, 4, 2, 3, 0],
			[2, 5, 3, 4, 1],
			[0, 0, 0, 0, 0]]
		*/

            if (m == null || m.length == 0) {
                return 0;
            }


            int row = m.length;
            int col = m[0].length;

            // build dp, dp[i][j]就是当前的第j列的，从上面开始到第i行连续1的个数
            int[][] dp = new int[row][col];

            // process first row
            for (int j = 0; j < col; j++) {
                dp[0][j] = m[0][j] - '0';
            }

            //@note: assumption, at least 2 rows
            for (int i = 1; i < row; i++) {
                for (int j = 0; j < col; j++) {
                    if (m[i][j] - '0' != 0) {
                        dp[i][j] = 1 + dp[i - 1][j];
                    }
                }
            }

            if (m.length == 1) {
                return findRowMax(dp[0]);
            }


            // search each row of dp array
            int max = 0;
            for (int i = 0; i < row; i++) {
                int rowMax = findRowMax(dp[i]);
                max = max > rowMax ? max : rowMax;
            }

            return max;
        }

        public int findRowMax(int[] rowOriginal) {

            int[] row = new int[rowOriginal.length + 1];
            row = Arrays.copyOfRange(rowOriginal, 0, rowOriginal.length + 1);

            int max = 0;
            int length = row.length;

            // stack store index, not the actual value
            Stack<Integer> sk = new Stack<>();
            int i = 0;
            while (i < length) {
                // if (i == 0 || row[i] >= row[sk.peek()]) {
                if (sk.isEmpty() || row[i] >= row[sk.peek()]) {
                    sk.push(i);
                    i++;
                } else {

                    // while (!sk.isEmpty() && row[i] < row[sk.peek()]) {

                    //     int index = sk.pop();
                    //     int prevIndex = sk.isEmpty()? 0 : sk.peek();

                    //     int area = (i - 1 - prevIndex) * row[index]; // i-1 is the highest bar before i
                    //     max = max > area ? max : area;

                    // }

                    int index = sk.pop();
                    // int prevIndex = sk.isEmpty()? 0 : sk.peek();
                    // int prevIndex = sk.isEmpty() ? i : sk.peek();

                    // 这里是：高度(row[index]) * 长度
                    int area = (sk.isEmpty() ? i : (i - 1 - sk.peek())) * row[index]; // i-1 is the highest bar before i
                    max = max > area ? max : area;

                    // sk.push(i++);
                }
            }

            // final check when reaching end of array. OR add dummy number to array end
            // while (!sk.isEmpty()) {

            //     int index = sk.pop();
            //     int prevIndex = sk.isEmpty()? 0 : sk.peek();

            //     int area = (i - 1 - prevIndex) * row[index]; // i-1 is the highest bar before i
            //     max = max > area ? max : area;
            // }

            return max;
        }
    }

}

############

class Solution {
    public int maximalRectangle(char[][] matrix) {
        int n = matrix[0].length;
        int[] heights = new int[n];
        int ans = 0;
        for (var row : matrix) {
            for (int j = 0; j < n; ++j) {
                if (row[j] == '1') {
                    heights[j] += 1;
                } else {
                    heights[j] = 0;
                }
            }
            ans = Math.max(ans, largestRectangleArea(heights));
        }
        return ans;
    }

    private int largestRectangleArea(int[] heights) {
        int res = 0, n = heights.length;
        Deque<Integer> stk = new ArrayDeque<>();
        int[] left = new int[n];
        int[] right = new int[n];
        Arrays.fill(right, n);
        for (int i = 0; i < n; ++i) {
            while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) {
                right[stk.pop()] = i;
            }
            left[i] = stk.isEmpty() ? -1 : stk.peek();
            stk.push(i);
        }
        for (int i = 0; i < n; ++i) {
            res = Math.max(res, heights[i] * (right[i] - left[i] - 1));
        }
        return res;
    }
}

// OJ: https://leetcode.com/problems/maximal-rectangle/
// Time: O(MN)
// Space: O(N)
class Solution {
public:
    int maximalRectangle(vector<vector<char>>& A) {
        int M = A.size(), N = A[0].size(), ans = 0;
        vector<int> h(N), nextSmaller(N);
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) {
                h[j] = A[i][j] == '0' ? 0 : (h[j] + 1);
            }
            stack<int> s;
            for (int j = N - 1; j >= 0; --j) {
                while (s.size() && h[j] <= h[s.top()]) s.pop();
                nextSmaller[j] = s.size() ? s.top() : N;
                s.push(j);
            }
            s = {};
            for (int j = 0; j < N; ++j) {
                while (s.size() && h[j] <= h[s.top()]) s.pop();
                int prevSmaller = s.size() ? s.top() : -1;
                ans = max(ans, (nextSmaller[j] - prevSmaller - 1) * h[j]);
                s.push(j);
            }
        }
        return ans;
    }
};

class Solution:
    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        heights = [0] * len(matrix[0])
        ans = 0
        for row in matrix:
            for j, v in enumerate(row):
                if v == "1":
                    heights[j] += 1 # inherite from row above
                else:
                    heights[j] = 0
            # check for every row
            ans = max(ans, self.largestRectangleArea(heights))
        return ans

    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        stk = []
        left = [-1] * n
        right = [n] * n
        for i, h in enumerate(heights):
            while stk and heights[stk[-1]] >= h:
                stk.pop()
            if stk:
                left[i] = stk[-1]
            stk.append(i)
        return max(h * (right[i] - left[i] - 1) for i, h in enumerate(heights))

############

class Solution(object):
  def maximalRectangle(self, matrix):
    """
    :type matrix: List[List[str]]
    :rtype: int
    """

    def histogram(height):
      if not height:
        return 0
      height.append(-1)
      stack = []
      ans = 0
      for i in range(0, len(height)):
        while stack and height[i] < height[stack[-1]]:
          h = height[stack.pop()]
          w = i - stack[-1] - 1 if stack else i
          ans = max(ans, h * w)
        stack.append(i)
      return ans

    ans = 0
    dp = [[0] * len(matrix[0]) for _ in range(0, len(matrix))]
    for i in reversed(range(0, len(matrix))):
      if i == len(matrix) - 1:
        dp[i] = [int(h) for h in matrix[i]]
      else:
        for j in range(0, len(matrix[0])):
          if matrix[i][j] != "0":
            dp[i][j] = dp[i + 1][j] + 1
      ans = max(ans, histogram(dp[i]))
    return ans

func maximalRectangle(matrix [][]byte) int {
	n := len(matrix[0])
	heights := make([]int, n)
	ans := 0
	for _, row := range matrix {
		for j, v := range row {
			if v == '1' {
				heights[j]++
			} else {
				heights[j] = 0
			}
		}
		ans = max(ans, largestRectangleArea(heights))
	}
	return ans
}

func largestRectangleArea(heights []int) int {
	res, n := 0, len(heights)
	var stk []int
	left, right := make([]int, n), make([]int, n)
	for i := range right {
		right[i] = n
	}
	for i, h := range heights {
		for len(stk) > 0 && heights[stk[len(stk)-1]] >= h {
			right[stk[len(stk)-1]] = i
			stk = stk[:len(stk)-1]
		}
		if len(stk) > 0 {
			left[i] = stk[len(stk)-1]
		} else {
			left[i] = -1
		}
		stk = append(stk, i)
	}
	for i, h := range heights {
		res = max(res, h*(right[i]-left[i]-1))
	}
	return res
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

using System;
using System.Collections.Generic;
using System.Linq;

public class Solution {
    private int MaximalRectangleHistagram(int[] height) {
        var stack = new Stack<int>();
        var result = 0;
        var i = 0;
        while (i < height.Length || stack.Any())
        {
            if (!stack.Any() || (i < height.Length && height[stack.Peek()] < height[i]))
            {
                stack.Push(i);
                ++i;
            }
            else
            {
                var previousIndex = stack.Pop();
                var area = height[previousIndex] * (stack.Any() ? (i - stack.Peek() - 1) : i);
                result = Math.Max(result, area);
            }
        }

        return result;
    }

    public int MaximalRectangle(char[][] matrix) {
        var lenI = matrix.Length;
        var lenJ = lenI == 0 ? 0 : matrix[0].Length;
        var height = new int[lenJ];
        var result = 0;
        for (var i = 0; i < lenI; ++i)
        {
            for (var j = 0; j < lenJ; ++j)
            {
                if (matrix[i][j] == '1')
                {
                    ++height[j];
                }
                else
                {
                    height[j] = 0;
                }
            }
            result = Math.Max(result, MaximalRectangleHistagram(height));
        }
        return result;
    }
}

impl Solution {
    #[allow(dead_code)]
    pub fn maximal_rectangle(matrix: Vec<Vec<char>>) -> i32 {
        let n = matrix[0].len();
        let mut heights = vec![0; n];
        let mut ret = -1;

        for row in &matrix {
            Self::array_builder(row, &mut heights);
            ret = std::cmp::max(ret, Self::largest_rectangle_area(heights.clone()));
        }

        ret
    }

    /// Helper function, build the heights array according to the input
    #[allow(dead_code)]
    fn array_builder(input: &Vec<char>, heights: &mut Vec<i32>) {
        for (i, &c) in input.iter().enumerate() {
            heights[i] += match c {
                '1' => 1,
                '0' => {
                    heights[i] = 0;
                    0
                }
                _ => panic!("This is impossible"),
            };
        }
    }

    /// Helper function, see: https://leetcode.com/problems/largest-rectangle-in-histogram/ for details
    #[allow(dead_code)]
    fn largest_rectangle_area(heights: Vec<i32>) -> i32 {
        let n = heights.len();
        let mut left = vec![-1; n];
        let mut right = vec![-1; n];
        let mut stack: Vec<(usize, i32)> = Vec::new();
        let mut ret = -1;

        // Build left vector
        for (i, h) in heights.iter().enumerate() {
            while !stack.is_empty() && stack.last().unwrap().1 >= *h {
                stack.pop();
            }
            if stack.is_empty() {
                left[i] = -1;
            } else {
                left[i] = stack.last().unwrap().0 as i32;
            }
            stack.push((i, *h));
        }

        stack.clear();

        // Build right vector
        for (i, h) in heights.iter().enumerate().rev() {
            while !stack.is_empty() && stack.last().unwrap().1 >= *h {
                stack.pop();
            }
            if stack.is_empty() {
                right[i] = n as i32;
            } else {
                right[i] = stack.last().unwrap().0 as i32;
            }
            stack.push((i, *h));
        }

        // Calculate the max area
        for (i, h) in heights.iter().enumerate() {
            ret = std::cmp::max(ret, (right[i] - left[i] - 1) * *h);
        }

        ret
    }
}

85 - Maximal Rectangle

Question

Algorithm

Code

All Problems

All Solutions

Welcome to Subscribe On Youtube

Question

Algorithm

Code

All Problems

All Solutions