Welcome to Subscribe On Youtube
84. Largest Rectangle in Histogram
Description
Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.
Example 1:
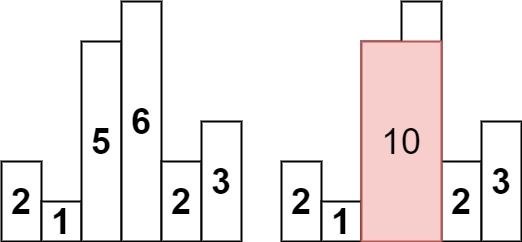
Input: heights = [2,1,5,6,2,3] Output: 10 Explanation: The above is a histogram where width of each bar is 1. The largest rectangle is shown in the red area, which has an area = 10 units.
Example 2:
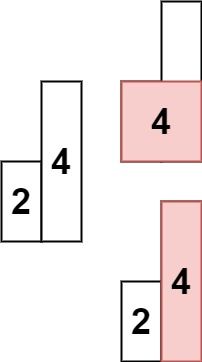
Input: heights = [2,4] Output: 4
Constraints:
1 <= heights.length <= 1050 <= heights[i] <= 104
Solutions
Solution 1: Monotonic Stack
We can enumerate the height $h$ of each bar as the height of the rectangle. Using a monotonic stack, we find the index $left_i$, $right_i$ of the first bar with a height less than $h$ to the left and right. The area of the rectangle at this time is $h \times (right_i-left_i-1)$. We can find the maximum value.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ represents the length of $heights$.
Common model of monotonic stack: Find the nearest number to the left/right of each number that is larger/smaller than it. Template:
stk = []
for i in range(n):
while stk and check(stk[-1], i):
stk.pop()
stk.append(i)
keyword: “Eliminate the shadow”, that is, the lowest bar is the length of a side
Intuitively, the area of the two bars depends on the shortest and lowest bar among them.
My own doubt is if it is [1,2,3,4,1,2,3,4].
How to prove that the first 1 and last 4 restricted rectangles will definitely not be the largest? Because the stack only maintains the current one, note that there is only one, an increasing sequence.
Simplified to [1,2,1,2], then the maximum area is the area 4 formed by the first 1 and the last 2
- So the key is that the push and pop conditions of the stack must ensure that the
lowest baris always in the stack.
Extend to eg. [3,1,2,1,2], the largest area also comes from the area formed by the first and last bar at 5.
Because the lowest one will always be in the stack, and the stack will eventually pop to empty, The last pop is the smallest bar. At this time, the shortest bar is multiplied by the length from the first to the last.
The whole question will be clear if you understand this: int currentWidth = sk.isEmpty()? i: (i-1-sk.peek());
sk.peek() is definitely the essence of the quintessence, to find the width of the largest rectangle, I wrote i-currentIndex at the beginning, but I ignored the situation when counting 4 in 2, 8, 8, 4, 6, 8. There are two 88 in front of 4, that is, the width should be from the first 8 to the last 8.
At this time, to find this width, you need sk.peek() to find the previous small index
There is another pit, which is the application of dummy end, which has the same effect as dummy head, allowing the for loop to start and run normally.
Arrays.copyOfRange(origin, start, end), if end exceeds the length of the origin array, 0 will be added automatically
The best test case:
- 2,1,2
- 2,0,2
- 2,0,2,1,2
-
class Solution { public int largestRectangleArea(int[] heights) { int res = 0, n = heights.length; Deque<Integer> stk = new ArrayDeque<>(); int[] left = new int[n]; int[] right = new int[n]; Arrays.fill(right, n); for (int i = 0; i < n; ++i) { while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) { right[stk.pop()] = i; } left[i] = stk.isEmpty() ? -1 : stk.peek(); stk.push(i); } for (int i = 0; i < n; ++i) { res = Math.max(res, heights[i] * (right[i] - left[i] - 1)); } return res; } } -
class Solution { public: int largestRectangleArea(vector<int>& heights) { int res = 0, n = heights.size(); stack<int> stk; vector<int> left(n, -1); vector<int> right(n, n); for (int i = 0; i < n; ++i) { while (!stk.empty() && heights[stk.top()] >= heights[i]) { right[stk.top()] = i; stk.pop(); } if (!stk.empty()) left[i] = stk.top(); stk.push(i); } for (int i = 0; i < n; ++i) res = max(res, heights[i] * (right[i] - left[i] - 1)); return res; } }; -
''' 枚举每根柱子的高度 h 作为矩形的高度,向左右两边找第一个高度 小于(<) h 的下标 left_i, right_i 那么此时矩形面积为 h * (right_i - left_i - 1),求最大值即可。 ''' class Solution: def largestRectangleArea(self, heights: List[int]) -> int: n = len(heights) stk = [] left = [-1] * n right = [n] * n for i, h in enumerate(heights): while stk and heights[stk[-1]] >= h: right[stk[-1]] = i stk.pop() if stk: left[i] = stk[-1] # same as below: stk[-1] in 'i - stack[-1] - 1' stk.append(i) # valid for one element input [3] return max(h * (right[i] - left[i] - 1) for i, h in enumerate(heights)) ############ class Solution: def largestRectangleArea(self, heights: List[int]) -> int: if not heights: return 0 heights.append(-1) # make for loop running stack = [] ans = 0 for i in range(0, len(heights)): while stack and heights[i] < heights[stack[-1]]: currentLowestBarIndex = stack.pop() h = heights[currentLowestBarIndex] # stack[-1] is after pop(). why not i-currentLowestBarIndex? # because not working for tie case in the stack, # eg. for input=[4,2,0,3,2,5], expected=6 but output=5 # 向左右两边找第一个高度 小于(<) h 的下标 left_i, right_i # 如果是左右两边都是 大于 h 的下标,那么宽度是 right-left+1 # 但是这里是 小于 h的下标,right-left+1 情况 向左向右 都拓展一个index,多了两个,+1 -2 得 -1 w = i - stack[-1] - 1 if stack else i ans = max(ans, h * w) stack.append(i) heights.pop() # restore, pop -1 return ans -
func largestRectangleArea(heights []int) int { res, n := 0, len(heights) var stk []int left, right := make([]int, n), make([]int, n) for i := range right { right[i] = n } for i, h := range heights { for len(stk) > 0 && heights[stk[len(stk)-1]] >= h { right[stk[len(stk)-1]] = i stk = stk[:len(stk)-1] } if len(stk) > 0 { left[i] = stk[len(stk)-1] } else { left[i] = -1 } stk = append(stk, i) } for i, h := range heights { res = max(res, h*(right[i]-left[i]-1)) } return res } -
using System; using System.Collections.Generic; using System.Linq; public class Solution { public int LargestRectangleArea(int[] height) { var stack = new Stack<int>(); var result = 0; var i = 0; while (i < height.Length || stack.Any()) { if (!stack.Any() || (i < height.Length && height[stack.Peek()] < height[i])) { stack.Push(i); ++i; } else { var previousIndex = stack.Pop(); var area = height[previousIndex] * (stack.Any() ? (i - stack.Peek() - 1) : i); result = Math.Max(result, area); } } return result; } } -
impl Solution { #[allow(dead_code)] pub fn largest_rectangle_area(heights: Vec<i32>) -> i32 { let n = heights.len(); let mut left = vec![-1; n]; let mut right = vec![-1; n]; let mut stack: Vec<(usize, i32)> = Vec::new(); let mut ret = -1; // Build left vector for (i, h) in heights.iter().enumerate() { while !stack.is_empty() && stack.last().unwrap().1 >= *h { stack.pop(); } if stack.is_empty() { left[i] = -1; } else { left[i] = stack.last().unwrap().0 as i32; } stack.push((i, *h)); } stack.clear(); // Build right vector for (i, h) in heights.iter().enumerate().rev() { while !stack.is_empty() && stack.last().unwrap().1 >= *h { stack.pop(); } if stack.is_empty() { right[i] = n as i32; } else { right[i] = stack.last().unwrap().0 as i32; } stack.push((i, *h)); } // Calculate the max area for (i, h) in heights.iter().enumerate() { ret = std::cmp::max(ret, (right[i] - left[i] - 1) * *h); } ret } }