Welcome to Subscribe On Youtube
62. Unique Paths
Description
There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.
Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.
The test cases are generated so that the answer will be less than or equal to 2 * 109.
Example 1:
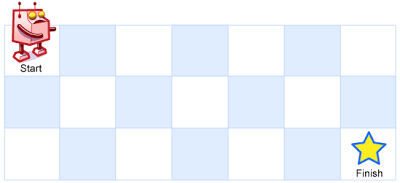
Input: m = 3, n = 7 Output: 28
Example 2:
Input: m = 3, n = 2 Output: 3 Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner: 1. Right -> Down -> Down 2. Down -> Down -> Right 3. Down -> Right -> Down
Constraints:
1 <= m, n <= 100
Solutions
Solution 1: Dynamic Programming
We define $f[i][j]$ to represent the number of paths from the top left corner to $(i, j)$, initially $f[0][0] = 1$, and the answer is $f[m - 1][n - 1]$.
Consider $f[i][j]$:
- If $i > 0$, then $f[i][j]$ can be reached by taking one step from $f[i - 1][j]$, so $f[i][j] = f[i][j] + f[i - 1][j]$;
- If $j > 0$, then $f[i][j]$ can be reached by taking one step from $f[i][j - 1]$, so $f[i][j] = f[i][j] + f[i][j - 1]$.
Therefore, we have the following state transition equation:
\[f[i][j] = \begin{cases} 1 & i = 0, j = 0 \\ f[i - 1][j] + f[i][j - 1] & \text{otherwise} \end{cases}\]The final answer is $f[m - 1][n - 1]$.
The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the number of rows and columns of the grid, respectively.
We notice that $f[i][j]$ is only related to $f[i - 1][j]$ and $f[i][j - 1]$, so we can optimize the first dimension space and only keep the second dimension space, resulting in a time complexity of $O(m \times n)$ and a space complexity of $O(n)$.
-
class Solution { public int uniquePaths(int m, int n) { int[] f = new int[n]; Arrays.fill(f, 1); for (int i = 1; i < m; ++i) { for (int j = 1; j < n; ++j) { f[j] += f[j - 1]; } } return f[n - 1]; } } -
class Solution { public: int uniquePaths(int m, int n) { vector<int> f(n, 1); for (int i = 1; i < m; ++i) { for (int j = 1; j < n; ++j) { f[j] += f[j - 1]; } } return f[n - 1]; } }; -
class Solution: def uniquePaths(self, m: int, n: int) -> int: # avoid setting dp[][] to 1 for i==0 or j==0 as initialization dp = [[1] * n for _ in range(m)] for i in range(1, m): for j in range(1, n): dp[i][j] = dp[i - 1][j] + dp[i][j - 1] return dp[-1][-1] -
func uniquePaths(m int, n int) int { f := make([]int, n+1) for i := range f { f[i] = 1 } for i := 1; i < m; i++ { for j := 1; j < n; j++ { f[j] += f[j-1] } } return f[n-1] } -
function uniquePaths(m: number, n: number): number { const f: number[] = Array(n).fill(1); for (let i = 1; i < m; ++i) { for (let j = 1; j < n; ++j) { f[j] += f[j - 1]; } } return f[n - 1]; } -
/** * @param {number} m * @param {number} n * @return {number} */ var uniquePaths = function (m, n) { const f = Array(n).fill(1); for (let i = 1; i < m; ++i) { for (let j = 1; j < n; ++j) { f[j] += f[j - 1]; } } return f[n - 1]; }; -
impl Solution { pub fn unique_paths(m: i32, n: i32) -> i32 { let (m, n) = (m as usize, n as usize); let mut f = vec![1; n]; for i in 1..m { for j in 1..n { f[j] += f[j - 1]; } } f[n - 1] } }