52. N-Queens II

Description

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return the number of distinct solutions to the n-queens puzzle.

Example 1:

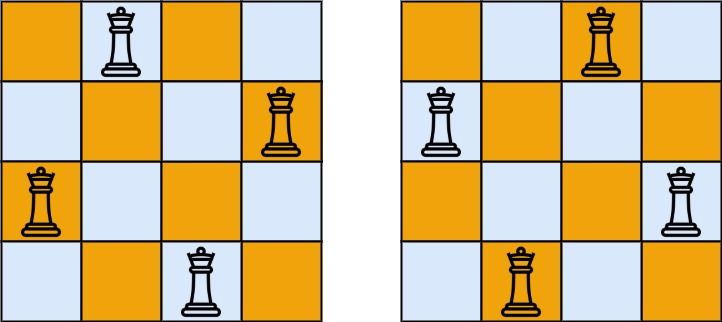
Input: n = 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown.

Example 2:

Input: n = 1
Output: 1

Constraints:

1 <= n <= 9

Solutions

Solution 1: Backtracking

We design a function $dfs(i)$, which represents starting the search from the $i$th row, and the results of the search are added to the answer.

In the $i$th row, we enumerate each column of the $i$th row. If the current column does not conflict with the queens placed before, then we can place a queen, and then continue to search the next row, that is, call $dfs(i + 1)$.

If a conflict occurs, then we skip the current column and continue to enumerate the next column.

To determine whether a conflict occurs, we need to use three arrays to record whether a queen has been placed in each column, each positive diagonal, and each negative diagonal, respectively.

Specifically, we use the $cols$ array to record whether a queen has been placed in each column, the $dg$ array to record whether a queen has been placed in each positive diagonal, and the $udg$ array to record whether a queen has been placed in each negative diagonal.

The time complexity is $O(n!)$, and the space complexity is $O(n)$. Here, $n$ is the number of queens.

class Solution {
    private int n;
    private int ans;
    private boolean[] cols = new boolean[10];
    private boolean[] dg = new boolean[20];
    private boolean[] udg = new boolean[20];

    public int totalNQueens(int n) {
        this.n = n;
        dfs(0);
        return ans;
    }

    private void dfs(int i) {
        if (i == n) {
            ++ans;
            return;
        }
        for (int j = 0; j < n; ++j) {
            int a = i + j, b = i - j + n;
            if (cols[j] || dg[a] || udg[b]) {
                continue;
            }
            cols[j] = true;
            dg[a] = true;
            udg[b] = true;
            dfs(i + 1);
            cols[j] = false;
            dg[a] = false;
            udg[b] = false;
        }
    }
}

class Solution {
public:
    int totalNQueens(int n) {
        bitset<10> cols;
        bitset<20> dg;
        bitset<20> udg;
        int ans = 0;
        function<void(int)> dfs = [&](int i) {
            if (i == n) {
                ++ans;
                return;
            }
            for (int j = 0; j < n; ++j) {
                int a = i + j, b = i - j + n;
                if (cols[j] || dg[a] || udg[b]) continue;
                cols[j] = dg[a] = udg[b] = 1;
                dfs(i + 1);
                cols[j] = dg[a] = udg[b] = 0;
            }
        };
        dfs(0);
        return ans;
    }
};

class Solution:
    def totalNQueens(self, n: int) -> int:
        def dfs(i: int):
            if i == n:
                nonlocal ans
                ans += 1
                return
            for j in range(n):
                a, b = i + j, i - j + n
                if cols[j] or dg[a] or udg[b]:
                    continue
                cols[j] = dg[a] = udg[b] = True
                dfs(i + 1)
                cols[j] = dg[a] = udg[b] = False

        cols = [False] * 10
        dg = [False] * 20
        udg = [False] * 20
        ans = 0
        dfs(0)
        return ans

func totalNQueens(n int) (ans int) {
	cols := [10]bool{}
	dg := [20]bool{}
	udg := [20]bool{}
	var dfs func(int)
	dfs = func(i int) {
		if i == n {
			ans++
			return
		}
		for j := 0; j < n; j++ {
			a, b := i+j, i-j+n
			if cols[j] || dg[a] || udg[b] {
				continue
			}
			cols[j], dg[a], udg[b] = true, true, true
			dfs(i + 1)
			cols[j], dg[a], udg[b] = false, false, false
		}
	}
	dfs(0)
	return
}

function totalNQueens(n: number): number {
    const cols: boolean[] = Array(10).fill(false);
    const dg: boolean[] = Array(20).fill(false);
    const udg: boolean[] = Array(20).fill(false);
    let ans = 0;
    const dfs = (i: number) => {
        if (i === n) {
            ++ans;
            return;
        }
        for (let j = 0; j < n; ++j) {
            let [a, b] = [i + j, i - j + n];
            if (cols[j] || dg[a] || udg[b]) {
                continue;
            }
            cols[j] = dg[a] = udg[b] = true;
            dfs(i + 1);
            cols[j] = dg[a] = udg[b] = false;
        }
    };
    dfs(0);
    return ans;
}

public class Solution {
    public int TotalNQueens(int n) {
        bool[] cols = new bool[10];
        bool[] dg = new bool[20];
        bool[] udg = new bool[20];
        int ans = 0;

        void dfs(int i) {
            if (i == n) {
                ans++;
                return;
            }
            for (int j = 0; j < n; j++) {
                int a = i + j, b = i - j + n;
                if (cols[j] || dg[a] || udg[b]) {
                    continue;
                }
                cols[j] = dg[a] = udg[b] = true;
                dfs(i + 1);
                cols[j] = dg[a] = udg[b] = false;
            }
        }

        dfs(0);
        return ans;
    }
}

function totalNQueens(n) {
    const cols = Array(10).fill(false);
    const dg = Array(20).fill(false);
    const udg = Array(20).fill(false);
    let ans = 0;
    const dfs = i => {
        if (i === n) {
            ++ans;
            return;
        }
        for (let j = 0; j < n; ++j) {
            let [a, b] = [i + j, i - j + n];
            if (cols[j] || dg[a] || udg[b]) {
                continue;
            }
            cols[j] = dg[a] = udg[b] = true;
            dfs(i + 1);
            cols[j] = dg[a] = udg[b] = false;
        }
    };
    dfs(0);
    return ans;
}

52 - N-Queens II

52. N-Queens II

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

52. N-Queens II

Description

Solutions

All Problems

All Solutions