Welcome to Subscribe On Youtube
11. Container With Most Water
Description
You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
Notice that you may not slant the container.
Example 1:
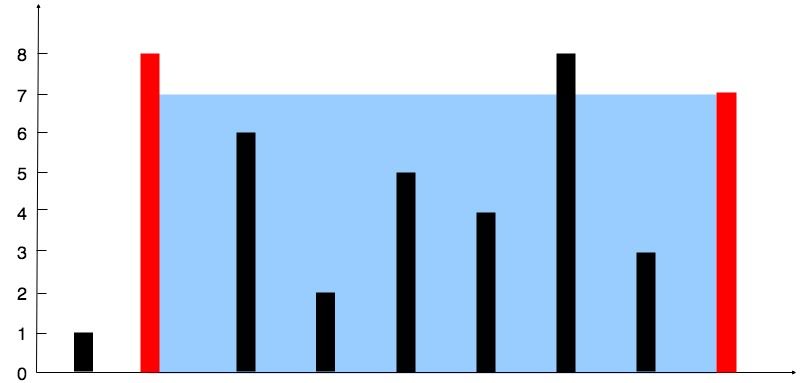
Input: height = [1,8,6,2,5,4,8,3,7] Output: 49 Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example 2:
Input: height = [1,1] Output: 1
Constraints:
n == height.length2 <= n <= 1050 <= height[i] <= 104
Solutions
Solution 1: Two Pointers
Initially, we consider the capacity of the water that the two farthest pillars can hold. The width of the water is the distance between the two pillars, and the height of the water depends on the shorter one between the two pillars.
The current pillars are the pillars on the farthest sides, so the width of the water is the largest. For other combinations, the width of the water is smaller. Suppose the height of the left pillar is less than or equal to the height of the right pillar, then the height of the water is the height of the left pillar. If we move the right pillar, the width of the water will decrease, but the height of the water will not increase, so the capacity of the water will definitely decrease. Therefore, we move the left pillar and update the maximum capacity.
Repeat this process until the two pillars meet.
The time complexity is $O(n)$, where $n$ is the length of the array height. The space complexity is $O(1)$.
-
class Solution { public int maxArea(int[] height) { int i = 0, j = height.length - 1; int ans = 0; while (i < j) { int t = Math.min(height[i], height[j]) * (j - i); ans = Math.max(ans, t); if (height[i] < height[j]) { ++i; } else { --j; } } return ans; } } -
class Solution { public: int maxArea(vector<int>& height) { int i = 0, j = height.size() - 1; int ans = 0; while (i < j) { int t = min(height[i], height[j]) * (j - i); ans = max(ans, t); if (height[i] < height[j]) { ++i; } else { --j; } } return ans; } }; -
class Solution: def maxArea(self, height: List[int]) -> int: i, j = 0, len(height) - 1 ans = 0 while i < j: t = (j - i) * min(height[i], height[j]) ans = max(ans, t) if height[i] < height[j]: i += 1 else: j -= 1 return ans -
func maxArea(height []int) (ans int) { i, j := 0, len(height)-1 for i < j { t := min(height[i], height[j]) * (j - i) ans = max(ans, t) if height[i] < height[j] { i++ } else { j-- } } return } -
function maxArea(height: number[]): number { let i = 0; let j = height.length - 1; let ans = 0; while (i < j) { const t = Math.min(height[i], height[j]) * (j - i); ans = Math.max(ans, t); if (height[i] < height[j]) { ++i; } else { --j; } } return ans; } -
/** * @param {number[]} height * @return {number} */ var maxArea = function (height) { let i = 0; let j = height.length - 1; let ans = 0; while (i < j) { const t = Math.min(height[i], height[j]) * (j - i); ans = Math.max(ans, t); if (height[i] < height[j]) { ++i; } else { --j; } } return ans; }; -
public class Solution { public int MaxArea(int[] height) { int i = 0, j = height.Length - 1; int ans = 0; while (i < j) { int t = Math.Min(height[i], height[j]) * (j - i); ans = Math.Max(ans, t); if (height[i] < height[j]) { ++i; } else { --j; } } return ans; } } -
impl Solution { pub fn max_area(height: Vec<i32>) -> i32 { let mut i = 0; let mut j = height.len() - 1; let mut res = 0; while i < j { res = res.max(height[i].min(height[j]) * ((j - i) as i32)); if height[i] <= height[j] { i += 1; } else { j -= 1; } } res } } -
class Solution { /** * @param int[] $height * @return int */ function maxArea($height) { $left = 0; $right = count($height) - 1; $maxArea = 0; while ($left < $right) { $area = min($height[$left], $height[$right]) * ($right - $left); $maxArea = max($maxArea, $area); if ($height[$left] < $height[$right]) { $left++; } else { $right--; } } return $maxArea; } }