1059. All Paths from Source Lead to Destination

Given the edges of a directed graph, and two nodes source and destination of this graph, determine whether or not all paths starting from source eventually end at destination, that is:

• At least one path exists from the source node to the destination node
• If a path exists from the source node to a node with no outgoing edges, then that node is equal to destination.
• The number of possible paths from source to destination is a finite number.

Return true if and only if all roads from source lead to destination.

Example 1:

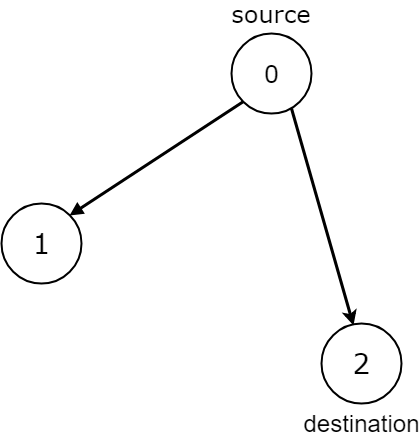
Input: n = 3, edges = [[0,1],[0,2]], source = 0, destination = 2
Output: false
Explanation: It is possible to reach and get stuck on both node 1 and node 2.

Example 2:

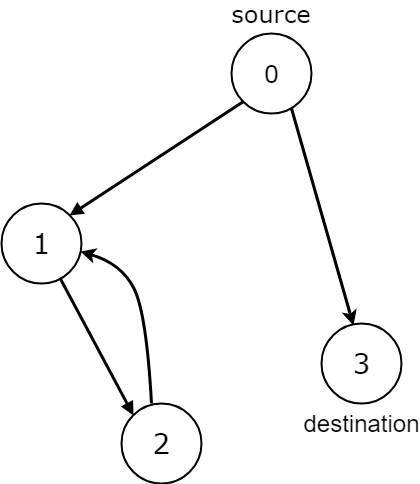
Input: n = 4, edges = [[0,1],[0,3],[1,2],[2,1]], source = 0, destination = 3
Output: false
Explanation: We have two possibilities: to end at node 3, or to loop over node 1 and node 2 indefinitely.

Example 3:

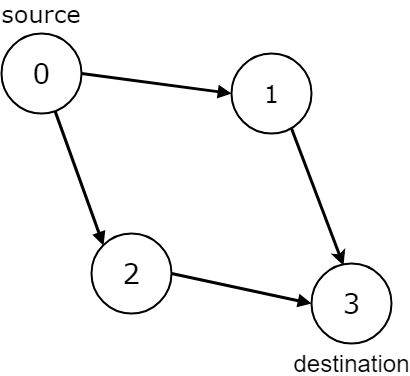
Input: n = 4, edges = [[0,1],[0,2],[1,3],[2,3]], source = 0, destination = 3
Output: true

Example 4:

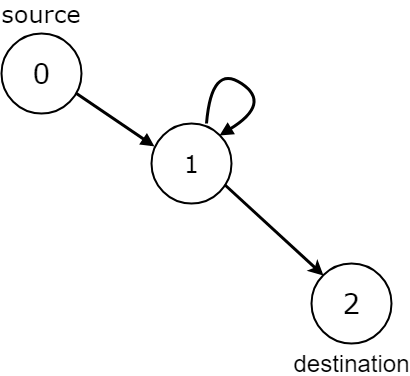
Input: n = 3, edges = [[0,1],[1,1],[1,2]], source = 0, destination = 2
Output: false
Explanation: All paths from the source node end at the destination node, but there are an infinite number of paths, such as 0-1-2, 0-1-1-2, 0-1-1-1-2, 0-1-1-1-1-2, and so on.

Example 5:

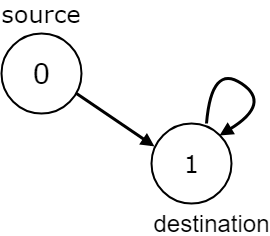
Input: n = 2, edges = [[0,1],[1,1]], source = 0, destination = 1
Output: false
Explanation: There is infinite self-loop at destination node.

Note:

1. The given graph may have self loops and parallel edges.
2. The number of nodes n in the graph is between 1 and 10000
3. The number of edges in the graph is between 0 and 10000
4. 0 <= edges.length <= 10000
5. edges[i].length == 2
6. 0 <= source <= n - 1
7. 0 <= destination <= n - 1