1059. All Paths from Source Lead to Destination

Description

Given the edges of a directed graph where edges[i] = [a_i, b_i] indicates there is an edge between nodes a_i and b_i, and two nodes source and destination of this graph, determine whether or not all paths starting from source eventually, end at destination, that is:

At least one path exists from the source node to the destination node
If a path exists from the source node to a node with no outgoing edges, then that node is equal to destination.
The number of possible paths from source to destination is a finite number.

Return true if and only if all roads from source lead to destination.

Example 1:

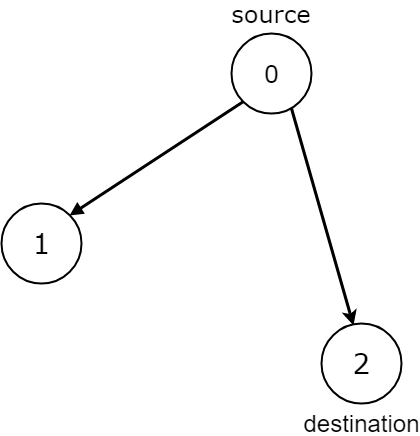
Input: n = 3, edges = [[0,1],[0,2]], source = 0, destination = 2
Output: false
Explanation: It is possible to reach and get stuck on both node 1 and node 2.

Example 2:

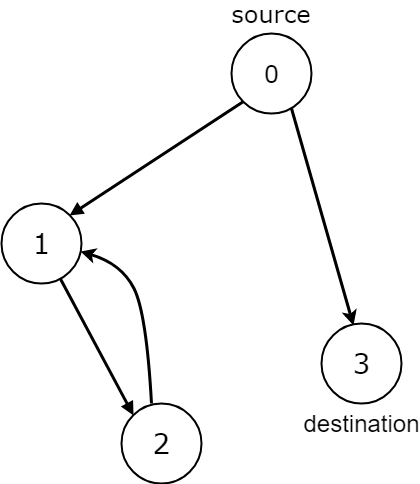
Input: n = 4, edges = [[0,1],[0,3],[1,2],[2,1]], source = 0, destination = 3
Output: false
Explanation: We have two possibilities: to end at node 3, or to loop over node 1 and node 2 indefinitely.

Example 3:

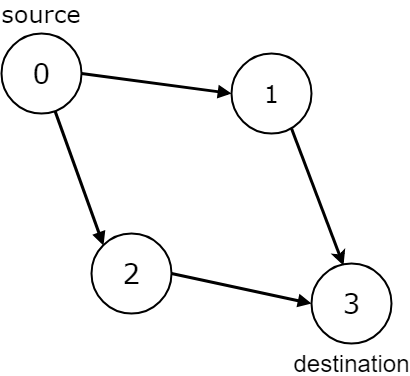
Input: n = 4, edges = [[0,1],[0,2],[1,3],[2,3]], source = 0, destination = 3
Output: true

Constraints:

1 <= n <= 10⁴
0 <= edges.length <= 10⁴
edges.length == 2
0 <= a_i, b_i <= n - 1
0 <= source <= n - 1
0 <= destination <= n - 1
The given graph may have self-loops and parallel edges.

Solutions

There are 2 cases it should return false.

case 1: it encounters a node that has no outgoing edges, but it is not destination.
case 2: it has cycle.

Otherwise, it returns true.

Could iterate graph with BFS. When indegree of a node becomes negative, then ther is cycle.

Time Complexity: O(n+e)

e = edges.length.

Space: O(n+e).

class Solution {
    private List<Integer>[] g;
    private int[] f;
    private boolean[] vis;
    private int k;

    public boolean leadsToDestination(int n, int[][] edges, int source, int destination) {
        vis = new boolean[n];
        g = new List[n];
        k = destination;
        f = new int[n];
        Arrays.setAll(g, key -> new ArrayList<>());
        for (var e : edges) {
            g[e[0]].add(e[1]);
        }
        return dfs(source);
    }

    private boolean dfs(int i) {
        if (i == k) {
            return g[i].isEmpty();
        }
        if (f[i] != 0) {
            return f[i] == 1;
        }
        if (vis[i] || g[i].isEmpty()) {
            return false;
        }
        vis[i] = true;
        for (int j : g[i]) {
            if (!dfs(j)) {
                f[i] = -1;
                return false;
            }
        }
        f[i] = 1;
        return true;
    }
}

//////

public class All_Paths_from_Source_Lead_to_Destination {

    class Solution_bfs {
        public boolean leadsToDestination(int n, int[][] edges, int source, int destination) {
            Set<Integer>[] graph = new Set[n]; // node => set of its next nodes

            for (int i = 0; i < n; i++) {
                graph[i] = new HashSet<Integer>();
            }

            int[] inDegrees = new int[n];
            for (int[] edge : edges) {
                graph[edge[0]].add(edge[1]);
                inDegrees[edge[1]]++;
            }

            LinkedList<Integer> q = new LinkedList<Integer>();
            q.add(source);

            while (!q.isEmpty()) {
                int cur = q.poll();
                if (graph[cur].size() == 0 && cur != destination) {
                    return false;
                }

                for (int nei : graph[cur]) {
                    if (inDegrees[nei] < 0) { // i.e. a cycle
                        return false;
                    }

                    inDegrees[nei]--;

                    q.add(nei);
                }
            }

            return true;
        }
    }

    class Solution_dfs {
        public boolean leadsToDestination(int n, int[][] edges, int source, int destination) {
            Map<Integer, Set<Integer>> graph = new HashMap<>();
            for (int[] edge : edges) {
                Set<Integer> neighbours = graph.getOrDefault(edge[0], new HashSet<>());
                neighbours.add(edge[1]);
                graph.put(edge[0], neighbours);
            }
            if (graph.get(destination) != null) return false;
            boolean[] isVisited = new boolean[n];
            isVisited[source] = true;
            return dfs(graph, isVisited, source, destination);
        }

        private boolean dfs(Map<Integer, Set<Integer>> graph, boolean[] isVisited, int source, int destination) {
            if (source == destination) {
                return true;
            }

            Set<Integer> neighbours = graph.getOrDefault(source, new HashSet<>());
            if (neighbours.size() == 0) return false;
            for (int neib : neighbours) {

                if (isVisited[neib]) return false; // cycle spotted

                isVisited[neib] = true;
                if (!dfs(graph, isVisited, neib, destination)) return false;
                isVisited[neib] = false;
            }
            return true;
        }
    }
}

class Solution {
public:
    bool leadsToDestination(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<bool> vis(n);
        vector<vector<int>> g(n);
        vector<int> f(n);
        for (auto& e : edges) {
            g[e[0]].push_back(e[1]);
        }
        function<bool(int)> dfs = [&](int i) {
            if (i == destination) {
                return g[i].empty();
            }
            if (f[i]) {
                return f[i] == 1;
            }
            if (vis[i] || g[i].empty()) {
                return false;
            }
            vis[i] = true;
            for (int j : g[i]) {
                if (!dfs(j)) {
                    f[i] = -1;
                    return false;
                }
            }
            f[i] = 1;
            return true;
        };
        return dfs(source);
    }
};

class Solution: # dfs
    def leadsToDestination(
        self, n: int, edges: List[List[int]], source: int, destination: int
    ) -> bool:
        @cache
        def dfs(i):
            if i == destination:
                return not g[i]
            if i in vis or not g[i]: # not g[i]: not destination but no more neigbours
                return False
            vis.add(i)
            for j in g[i]:
                if not dfs(j):
                    return False
            return True

        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
        vis = set()
        return dfs(source)


#########

from collections import defaultdict, deque

class Solution: # bfs
    def leadsToDestination(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        # Build the adjacency list representation of the graph
        graph = defaultdict(list)
        for u, v in edges:
            graph[u].append(v)

        # Handle the case where the destination node has outgoing edges
        if graph[destination]:
            return False

        # Initialize the visited array to keep track of visited nodes during the traversal
        visited = [False] * n

        # Start the BFS traversal from the source node
        queue = deque([source])
        visited[source] = True

        while queue:
            node = queue.popleft()

            # Check if the current node has no outgoing edges and is not the destination node
            if node != destination and not graph[node]:
                return False

            # Process the neighbors of the current node
            for neighbor in graph[node]:
                # If the neighbor has been visited before, it forms a cycle, return False
                if visited[neighbor]:
                    return False

                visited[neighbor] = True
                queue.append(neighbor)

                # Remove the edge to prevent revisiting the same node
                graph[node].remove(neighbor)

        # Check if all nodes (except the destination) have been visited
        # destination node may have outgoing edges in the graph, so exclude it
        return all(visited[i] for i in range(n) if i != destination)

func leadsToDestination(n int, edges [][]int, source int, destination int) bool {
	vis := make([]bool, n)
	g := make([][]int, n)
	f := make([]int, n)
	for _, e := range edges {
		g[e[0]] = append(g[e[0]], e[1])
	}
	var dfs func(int) bool
	dfs = func(i int) bool {
		if i == destination {
			return len(g[i]) == 0
		}
		if f[i] != 0 {
			return f[i] == 1
		}
		if vis[i] || len(g[i]) == 0 {
			return false
		}
		vis[i] = true
		for _, j := range g[i] {
			if !dfs(j) {
				f[i] = -1
				return false
			}
		}
		f[i] = 1
		return true
	}
	return dfs(source)
}

1059 - All Paths from Source Lead to Destination

1059. All Paths from Source Lead to Destination

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1059. All Paths from Source Lead to Destination

Description

Solutions

All Problems

All Solutions