3787. Find Diameter Endpoints of a Tree 🔒

Description

You are given an undirected tree with n nodes, numbered from 0 to n - 1. It is represented by a 2D integer array edges of length n - 1, where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree.

A node is called special if it is an endpoint of any diameter path of the tree.

Return a binary string s of length n, where s[i] = '1' if node i is special, and s[i] = '0' otherwise.

A diameter path of a tree is the longest simple path between any two nodes. A tree may have multiple diameter paths.

An endpoint of a path is the first or last node on that path.

Example 1:

Input: n = 3, edges = [[0,1],[1,2]]

Output: "101"

Explanation:

The diameter of this tree consists of 2 edges.
The only diameter path is the path from node 0 to node 2
The endpoints of this path are nodes 0 and 2, so they are special.

Example 2:

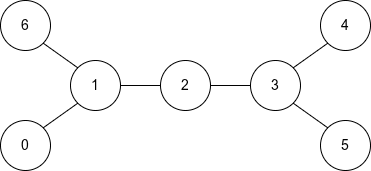
Input: n = 7, edges = [[0,1],[1,2],[2,3],[3,4],[3,5],[1,6]]

Output: "1000111"

Explanation:

The diameter of this tree consists of 4 edges. There are 4 diameter paths:

The path from node 0 to node 4
The path from node 0 to node 5
The path from node 6 to node 4
The path from node 6 to node 5

The special nodes are nodes 0, 4, 5, 6, as they are endpoints in at least one diameter path.

Example 3:

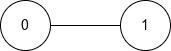
Input: n = 2, edges = [[0,1]]

Output: "11"

Explanation:

The diameter of this tree consists of 1 edge.
The only diameter path is the path from node 0 to node 1
The endpoints of this path are nodes 0 and 1, so they are special.

Constraints:

2 <= n <= 10⁵
edges.length == n - 1
edges[i] = [a_i, b_i]
0 <= a_i, b_i < n
The input is generated such that edges represents a valid tree.

Solutions

Solution 1: BFS

We first convert the array $\text{edges}$ into an adjacency list representation of an undirected graph, where $g[u]$ represents all nodes adjacent to node $u$.

Next, we can use Breadth-First Search (BFS) to find the diameter endpoints of the tree. The specific steps are as follows:

Starting from any node (e.g., node $0$), use BFS to find the farthest node $a$ from that node.
Starting from node $a$, use BFS again to find the farthest node $b$ from node $a$, as well as the distance array $\text{dist1}$ from node $a$ to all other nodes.
Starting from node $b$, use BFS to find the distance array $\text{dist2}$ from node $b$ to all other nodes.
The diameter length of the tree is $\text{dist1}[b]$. For each node $i$, if $\text{dist1}[i]$ or $\text{dist2}[i]$ equals the diameter length, then node $i$ is a special node.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes.

class Solution {
    public String findSpecialNodes(int n, int[][] edges) {
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (int[] e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }

        record BFSResult(int far, int[] dist) {
        }

        IntFunction<BFSResult> bfs = (int start) -> {
            int[] dist = new int[n];
            Arrays.fill(dist, -1);
            dist[start] = 0;
            ArrayDeque<Integer> q = new ArrayDeque<>();
            q.add(start);
            int far = start;
            while (!q.isEmpty()) {
                int u = q.poll();
                if (dist[u] > dist[far]) {
                    far = u;
                }
                for (int v : g[u]) {
                    if (dist[v] == -1) {
                        dist[v] = dist[u] + 1;
                        q.add(v);
                    }
                }
            }
            return new BFSResult(far, dist);
        };

        int a = bfs.apply(0).far();
        BFSResult r1 = bfs.apply(a);
        int b = r1.far();
        int[] dist1 = r1.dist();
        int[] dist2 = bfs.apply(b).dist();
        int d = dist1[b];

        char[] ans = new char[n];
        Arrays.fill(ans, '0');
        for (int i = 0; i < n; i++) {
            if (dist1[i] == d || dist2[i] == d) {
                ans[i] = '1';
            }
        }
        return new String(ans);
    }
}

class Solution {
public:
    string findSpecialNodes(int n, vector<vector<int>>& edges) {
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }

        auto bfs = [&](int start) -> pair<int, vector<int>> {
            vector<int> dist(n, -1);
            dist[start] = 0;
            deque<int> q;
            q.push_back(start);
            int far = start;
            while (!q.empty()) {
                int u = q.front();
                q.pop_front();
                if (dist[u] > dist[far]) {
                    far = u;
                }
                for (int v : g[u]) {
                    if (dist[v] == -1) {
                        dist[v] = dist[u] + 1;
                        q.push_back(v);
                    }
                }
            }
            return {far, dist};
        };

        auto [a, _0] = bfs(0);
        auto [b, dist1] = bfs(a);
        auto [_1, dist2] = bfs(b);
        int d = dist1[b];

        string ans(n, '0');
        for (int i = 0; i < n; i++) {
            if (dist1[i] == d || dist2[i] == d) {
                ans[i] = '1';
            }
        }
        return ans;
    }
};

class Solution:
    def findSpecialNodes(self, n: int, edges: List[List[int]]) -> str:
        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)

        def bfs(start: int):
            dist = [-1] * n
            dist[start] = 0
            q = deque([start])
            far = start
            while q:
                u = q.popleft()
                if dist[u] > dist[far]:
                    far = u
                for v in g[u]:
                    if dist[v] == -1:
                        dist[v] = dist[u] + 1
                        q.append(v)
            return far, dist

        a, _ = bfs(0)
        b, dist1 = bfs(a)
        _, dist2 = bfs(b)
        d = dist1[b]
        ans = ["0"] * n
        for i in range(n):
            if dist1[i] == d or dist2[i] == d:
                ans[i] = "1"
        return "".join(ans)

func findSpecialNodes(n int, edges [][]int) string {
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}

	bfs := func(start int) (int, []int) {
		dist := make([]int, n)
		for i := range dist {
			dist[i] = -1
		}
		dist[start] = 0
		q := make([]int, 0, n)
		q = append(q, start)
		far := start
		for head := 0; head < len(q); head++ {
			u := q[head]
			if dist[u] > dist[far] {
				far = u
			}
			for _, v := range g[u] {
				if dist[v] == -1 {
					dist[v] = dist[u] + 1
					q = append(q, v)
				}
			}
		}
		return far, dist
	}

	a, _ := bfs(0)
	b, dist1 := bfs(a)
	_, dist2 := bfs(b)
	d := dist1[b]

	ans := make([]byte, n)
	for i := range ans {
		ans[i] = '0'
	}
	for i := 0; i < n; i++ {
		if dist1[i] == d || dist2[i] == d {
			ans[i] = '1'
		}
	}
	return string(ans)
}

function findSpecialNodes(n: number, edges: number[][]): string {
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }

    const bfs = (start: number): [number, number[]] => {
        const dist = new Array<number>(n).fill(-1);
        dist[start] = 0;
        const q: number[] = [start];
        let far = start;

        for (const u of q) {
            if (dist[u] > dist[far]) {
                far = u;
            }
            for (const v of g[u]) {
                if (dist[v] === -1) {
                    dist[v] = dist[u] + 1;
                    q.push(v);
                }
            }
        }
        return [far, dist];
    };

    const [a] = bfs(0);
    const [b, dist1] = bfs(a);
    const [, dist2] = bfs(b);
    const d = dist1[b];

    const ans: string[] = new Array(n).fill('0');
    for (let i = 0; i < n; i++) {
        if (dist1[i] === d || dist2[i] === d) {
            ans[i] = '1';
        }
    }
    return ans.join('');
}

use std::collections::VecDeque;

impl Solution {
    pub fn find_special_nodes(n: i32, edges: Vec<Vec<i32>>) -> String {
        let n = n as usize;
        let mut g: Vec<Vec<usize>> = vec![vec![]; n];
        for e in edges {
            let a = e[0] as usize;
            let b = e[1] as usize;
            g[a].push(b);
            g[b].push(a);
        }

        fn bfs(start: usize, g: &Vec<Vec<usize>>) -> (usize, Vec<i32>) {
            let n = g.len();
            let mut dist = vec![-1i32; n];
            let mut q: VecDeque<usize> = VecDeque::new();
            dist[start] = 0;
            q.push_back(start);

            let mut far = start;
            while let Some(u) = q.pop_front() {
                if dist[u] > dist[far] {
                    far = u;
                }
                for &v in &g[u] {
                    if dist[v] == -1 {
                        dist[v] = dist[u] + 1;
                        q.push_back(v);
                    }
                }
            }
            (far, dist)
        }

        let (a, _) = bfs(0, &g);
        let (b, dist1) = bfs(a, &g);
        let (_, dist2) = bfs(b, &g);
        let d = dist1[b];

        let mut ans = vec![b'0'; n];
        for i in 0..n {
            if dist1[i] == d || dist2[i] == d {
                ans[i] = b'1';
            }
        }
        String::from_utf8(ans).unwrap()
    }
}

3787 - Find Diameter Endpoints of a Tree

3787. Find Diameter Endpoints of a Tree 🔒

Description

Solutions

Solution 1: BFS

All Problems

All Solutions

Welcome to Subscribe On Youtube

3787. Find Diameter Endpoints of a Tree 🔒

Description

Solutions

Solution 1: BFS

All Problems

All Solutions