Welcome to Subscribe On Youtube

3446. Sort Matrix by Diagonals

Description

You are given an n x n square matrix of integers grid. Return the matrix such that:

  • The diagonals in the bottom-left triangle (including the middle diagonal) are sorted in non-increasing order.
  • The diagonals in the top-right triangle are sorted in non-decreasing order.

 

Example 1:

Input: grid = [[1,7,3],[9,8,2],[4,5,6]]

Output: [[8,2,3],[9,6,7],[4,5,1]]

Explanation:

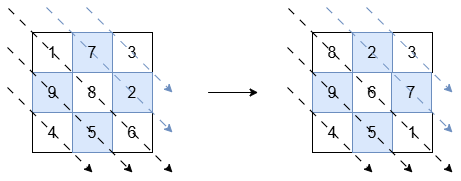
The diagonals with a black arrow (bottom-left triangle) should be sorted in non-increasing order:

  • [1, 8, 6] becomes [8, 6, 1].
  • [9, 5] and [4] remain unchanged.

The diagonals with a blue arrow (top-right triangle) should be sorted in non-decreasing order:

  • [7, 2] becomes [2, 7].
  • [3] remains unchanged.

Example 2:

Input: grid = [[0,1],[1,2]]

Output: [[2,1],[1,0]]

Explanation:

The diagonals with a black arrow must be non-increasing, so [0, 2] is changed to [2, 0]. The other diagonals are already in the correct order.

Example 3:

Input: grid = [[1]]

Output: [[1]]

Explanation:

Diagonals with exactly one element are already in order, so no changes are needed.

 

Constraints:

  • grid.length == grid[i].length == n
  • 1 <= n <= 10
  • -105 <= grid[i][j] <= 105

Solutions

Solution 1: Simulation + Sorting

We can simulate the diagonal sorting process as described in the problem.

First, we sort the diagonals of the lower-left triangle, including the main diagonal, in non-increasing order. Then, we sort the diagonals of the upper-right triangle in non-decreasing order. Finally, we return the sorted matrix.

The time complexity is O(n2logn), and the space complexity is O(n). Here, n is the size of the matrix.

  • class Solution {
    public int[][] sortMatrix(int[][] grid) {
        int n = grid.length;
        for (int k = n - 2; k >= 0; --k) {
            int i = k, j = 0;
            List<Integer> t = new ArrayList<>();
            while (i < n && j < n) {
                t.add(grid[i++][j++]);
            }
            Collections.sort(t);
            for (int x : t) {
                grid[--i][--j] = x;
            }
        }
        for (int k = n - 2; k > 0; --k) {
            int i = k, j = n - 1;
            List<Integer> t = new ArrayList<>();
            while (i >= 0 && j >= 0) {
                t.add(grid[i--][j--]);
            }
            Collections.sort(t);
            for (int x : t) {
                grid[++i][++j] = x;
            }
        }
        return grid;
    }
}


  • class Solution {
public:
    vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {
        int n = grid.size();
        for (int k = n - 2; k >= 0; --k) {
            int i = k, j = 0;
            vector<int> t;
            while (i < n && j < n) {
                t.push_back(grid[i++][j++]);
            }
            ranges::sort(t);
            for (int x : t) {
                grid[--i][--j] = x;
            }
        }
        for (int k = n - 2; k > 0; --k) {
            int i = k, j = n - 1;
            vector<int> t;
            while (i >= 0 && j >= 0) {
                t.push_back(grid[i--][j--]);
            }
            ranges::sort(t);
            for (int x : t) {
                grid[++i][++j] = x;
            }
        }
        return grid;
    }
};


  • class Solution:
    def sortMatrix(self, grid: List[List[int]]) -> List[List[int]]:
        n = len(grid)
        for k in range(n - 2, -1, -1):
            i, j = k, 0
            t = []
            while i < n and j < n:
                t.append(grid[i][j])
                i += 1
                j += 1
            t.sort()
            i, j = k, 0
            while i < n and j < n:
                grid[i][j] = t.pop()
                i += 1
                j += 1
        for k in range(n - 2, 0, -1):
            i, j = k, n - 1
            t = []
            while i >= 0 and j >= 0:
                t.append(grid[i][j])
                i -= 1
                j -= 1
            t.sort()
            i, j = k, n - 1
            while i >= 0 and j >= 0:
                grid[i][j] = t.pop()
                i -= 1
                j -= 1
        return grid


  • func sortMatrix(grid [][]int) [][]int {
	n := len(grid)
	for k := n - 2; k >= 0; k-- {
		i, j := k, 0
		t := []int{}
		for ; i < n && j < n; i, j = i+1, j+1 {
			t = append(t, grid[i][j])
		}
		sort.Ints(t)
		for _, x := range t {
			i, j = i-1, j-1
			grid[i][j] = x
		}
	}
	for k := n - 2; k > 0; k-- {
		i, j := k, n-1
		t := []int{}
		for ; i >= 0 && j >= 0; i, j = i-1, j-1 {
			t = append(t, grid[i][j])
		}
		sort.Ints(t)
		for _, x := range t {
			i, j = i+1, j+1
			grid[i][j] = x
		}
	}
	return grid
}


  • function sortMatrix(grid: number[][]): number[][] {
    const n = grid.length;
    for (let k = n - 2; k >= 0; --k) {
        let [i, j] = [k, 0];
        const t: number[] = [];
        while (i < n && j < n) {
            t.push(grid[i++][j++]);
        }
        t.sort((a, b) => a - b);
        for (const x of t) {
            grid[--i][--j] = x;
        }
    }
    for (let k = n - 2; k > 0; --k) {
        let [i, j] = [k, n - 1];
        const t: number[] = [];
        while (i >= 0 && j >= 0) {
            t.push(grid[i--][j--]);
        }
        t.sort((a, b) => a - b);
        for (const x of t) {
            grid[++i][++j] = x;
        }
    }
    return grid;
}

All Problems

All Solutions