Welcome to Subscribe On Youtube

3373. Maximize the Number of Target Nodes After Connecting Trees II

Description

There exist two undirected trees with n and m nodes, labeled from [0, n - 1] and [0, m - 1], respectively.

You are given two 2D integer arrays edges1 and edges2 of lengths n - 1 and m - 1, respectively, where edges1[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the first tree and edges2[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the second tree.

Node u is target to node v if the number of edges on the path from u to v is even. Note that a node is always target to itself.

Return an array of n integers answer, where answer[i] is the maximum possible number of nodes that are target to node i of the first tree if you had to connect one node from the first tree to another node in the second tree.

Note that queries are independent from each other. That is, for every query you will remove the added edge before proceeding to the next query.

 

Example 1:

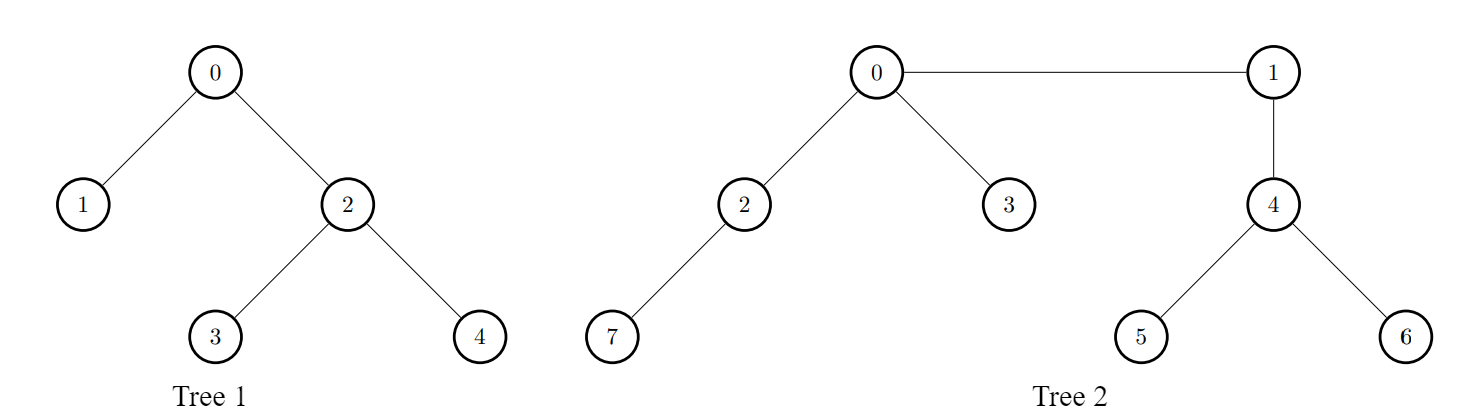
Input: edges1 = [[0,1],[0,2],[2,3],[2,4]], edges2 = [[0,1],[0,2],[0,3],[2,7],[1,4],[4,5],[4,6]]

Output: [8,7,7,8,8]

Explanation:

  • For i = 0, connect node 0 from the first tree to node 0 from the second tree.
  • For i = 1, connect node 1 from the first tree to node 4 from the second tree.
  • For i = 2, connect node 2 from the first tree to node 7 from the second tree.
  • For i = 3, connect node 3 from the first tree to node 0 from the second tree.
  • For i = 4, connect node 4 from the first tree to node 4 from the second tree.

Example 2:

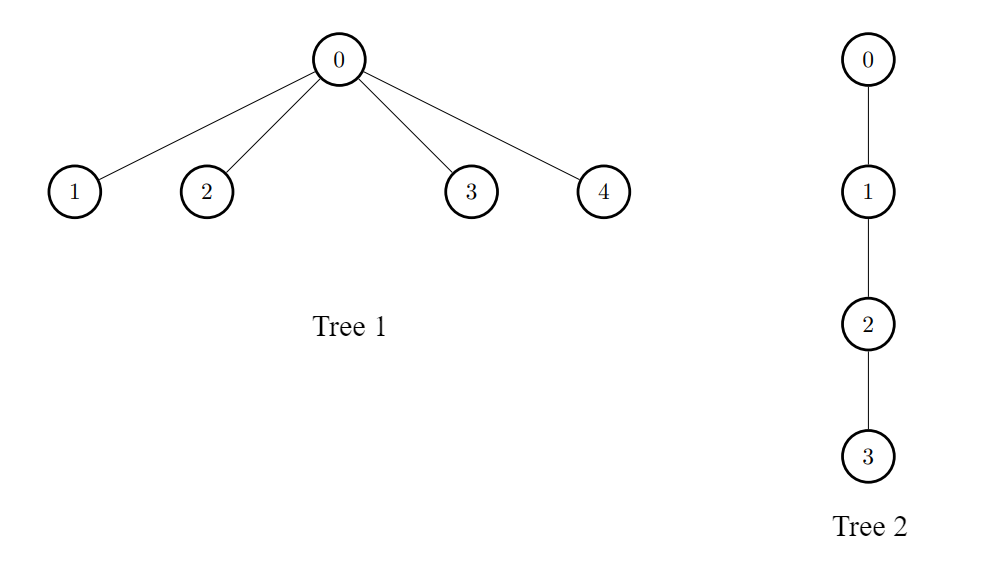
Input: edges1 = [[0,1],[0,2],[0,3],[0,4]], edges2 = [[0,1],[1,2],[2,3]]

Output: [3,6,6,6,6]

Explanation:

For every i, connect node i of the first tree with any node of the second tree.

 

Constraints:

  • 2 <= n, m <= 105
  • edges1.length == n - 1
  • edges2.length == m - 1
  • edges1[i].length == edges2[i].length == 2
  • edges1[i] = [ai, bi]
  • 0 <= ai, bi < n
  • edges2[i] = [ui, vi]
  • 0 <= ui, vi < m
  • The input is generated such that edges1 and edges2 represent valid trees.

Solutions

Solution 1: DFS

The number of target nodes for node $i$ can be divided into two parts:

  • The number of nodes in the first tree with the same depth parity as node $i$.
  • The maximum number of nodes in the second tree with the same depth parity.

First, we use Depth-First Search (DFS) to calculate the number of nodes in the second tree with the same depth parity, denoted as $\textit{cnt2}$. Then, we calculate the number of nodes in the first tree with the same depth parity as node $i$, denoted as $\textit{cnt1}$. Therefore, the number of target nodes for node $i$ is $\max(\textit{cnt2}) + \textit{cnt1}$.

The time complexity is $O(n + m)$, and the space complexity is $O(n + m)$. Here, $n$ and $m$ are the number of nodes in the first and second trees, respectively.

  • class Solution {
    public int[] maxTargetNodes(int[][] edges1, int[][] edges2) {
        var g1 = build(edges1);
        var g2 = build(edges2);
        int n = g1.length, m = g2.length;
        int[] c1 = new int[n];
        int[] c2 = new int[m];
        int[] cnt1 = new int[2];
        int[] cnt2 = new int[2];
        dfs(g2, 0, -1, c2, 0, cnt2);
        dfs(g1, 0, -1, c1, 0, cnt1);
        int t = Math.max(cnt2[0], cnt2[1]);
        int[] ans = new int[n];
        for (int i = 0; i < n; ++i) {
            ans[i] = t + cnt1[c1[i]];
        }
        return ans;
    }

    private List<Integer>[] build(int[][] edges) {
        int n = edges.length + 1;
        List<Integer>[] g = new List[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        return g;
    }

    private void dfs(List<Integer>[] g, int a, int fa, int[] c, int d, int[] cnt) {
        c[a] = d;
        cnt[d]++;
        for (int b : g[a]) {
            if (b != fa) {
                dfs(g, b, a, c, d ^ 1, cnt);
            }
        }
    }
}


  • class Solution {
public:
    vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2) {
        auto g1 = build(edges1);
        auto g2 = build(edges2);
        int n = g1.size(), m = g2.size();
        vector<int> c1(n, 0), c2(m, 0);
        vector<int> cnt1(2, 0), cnt2(2, 0);

        dfs(g2, 0, -1, c2, 0, cnt2);
        dfs(g1, 0, -1, c1, 0, cnt1);

        int t = max(cnt2[0], cnt2[1]);
        vector<int> ans(n);
        for (int i = 0; i < n; ++i) {
            ans[i] = t + cnt1[c1[i]];
        }
        return ans;
    }

private:
    vector<vector<int>> build(const vector<vector<int>>& edges) {
        int n = edges.size() + 1;
        vector<vector<int>> g(n);
        for (const auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        return g;
    }

    void dfs(const vector<vector<int>>& g, int a, int fa, vector<int>& c, int d, vector<int>& cnt) {
        c[a] = d;
        cnt[d]++;
        for (int b : g[a]) {
            if (b != fa) {
                dfs(g, b, a, c, d ^ 1, cnt);
            }
        }
    }
};


  • class Solution:
    def maxTargetNodes(
        self, edges1: List[List[int]], edges2: List[List[int]]
    ) -> List[int]:
        def build(edges: List[List[int]]) -> List[List[int]]:
            n = len(edges) + 1
            g = [[] for _ in range(n)]
            for a, b in edges:
                g[a].append(b)
                g[b].append(a)
            return g

        def dfs(
            g: List[List[int]], a: int, fa: int, c: List[int], d: int, cnt: List[int]
        ):
            c[a] = d
            cnt[d] += 1
            for b in g[a]:
                if b != fa:
                    dfs(g, b, a, c, d ^ 1, cnt)

        g1 = build(edges1)
        g2 = build(edges2)
        n, m = len(g1), len(g2)
        c1 = [0] * n
        c2 = [0] * m
        cnt1 = [0, 0]
        cnt2 = [0, 0]
        dfs(g2, 0, -1, c2, 0, cnt2)
        dfs(g1, 0, -1, c1, 0, cnt1)
        t = max(cnt2)
        return [t + cnt1[c1[i]] for i in range(n)]


  • func maxTargetNodes(edges1 [][]int, edges2 [][]int) []int {
    g1 := build(edges1)
    g2 := build(edges2)
    n, m := len(g1), len(g2)
    c1 := make([]int, n)
    c2 := make([]int, m)
    cnt1 := make([]int, 2)
    cnt2 := make([]int, 2)

    dfs(g2, 0, -1, c2, 0, cnt2)
    dfs(g1, 0, -1, c1, 0, cnt1)

    t := max(cnt2[0], cnt2[1])
    ans := make([]int, n)
    for i := 0; i < n; i++ {
        ans[i] = t + cnt1[c1[i]]
    }
    return ans
}

func build(edges [][]int) [][]int {
    n := len(edges) + 1
    g := make([][]int, n)
    for _, e := range edges {
        a, b := e[0], e[1]
        g[a] = append(g[a], b)
        g[b] = append(g[b], a)
    }
    return g
}

func dfs(g [][]int, a, fa int, c []int, d int, cnt []int) {
    c[a] = d
    cnt[d]++
    for _, b := range g[a] {
        if b != fa {
            dfs(g, b, a, c, d^1, cnt)
        }
    }
}


  • function maxTargetNodes(edges1: number[][], edges2: number[][]): number[] {
    const g1 = build(edges1);
    const g2 = build(edges2);
    const [n, m] = [g1.length, g2.length];
    const c1 = Array(n).fill(0);
    const c2 = Array(m).fill(0);
    const cnt1 = [0, 0];
    const cnt2 = [0, 0];

    dfs(g2, 0, -1, c2, 0, cnt2);
    dfs(g1, 0, -1, c1, 0, cnt1);

    const t = Math.max(...cnt2);
    const ans = Array(n);
    for (let i = 0; i < n; i++) {
        ans[i] = t + cnt1[c1[i]];
    }
    return ans;
}

function build(edges: number[][]): number[][] {
    const n = edges.length + 1;
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    return g;
}

function dfs(g: number[][], a: number, fa: number, c: number[], d: number, cnt: number[]): void {
    c[a] = d;
    cnt[d]++;
    for (const b of g[a]) {
        if (b !== fa) {
            dfs(g, b, a, c, d ^ 1, cnt);
        }
    }
}


  • public class Solution {
    public int[] MaxTargetNodes(int[][] edges1, int[][] edges2) {
        var g1 = Build(edges1);
        var g2 = Build(edges2);
        int n = g1.Length, m = g2.Length;
        var c1 = new int[n];
        var c2 = new int[m];
        var cnt1 = new int[2];
        var cnt2 = new int[2];

        Dfs(g2, 0, -1, c2, 0, cnt2);
        Dfs(g1, 0, -1, c1, 0, cnt1);

        int t = Math.Max(cnt2[0], cnt2[1]);
        var ans = new int[n];
        for (int i = 0; i < n; i++) {
            ans[i] = t + cnt1[c1[i]];
        }
        return ans;
    }

    private List<int>[] Build(int[][] edges) {
        int n = edges.Length + 1;
        var g = new List<int>[n];
        for (int i = 0; i < n; i++) {
            g[i] = new List<int>();
        }
        foreach (var e in edges) {
            int a = e[0], b = e[1];
            g[a].Add(b);
            g[b].Add(a);
        }
        return g;
    }

    private void Dfs(List<int>[] g, int a, int fa, int[] c, int d, int[] cnt) {
        c[a] = d;
        cnt[d]++;
        foreach (var b in g[a]) {
            if (b != fa) {
                Dfs(g, b, a, c, d ^ 1, cnt);
            }
        }
    }
}

All Problems

All Solutions