Welcome to Subscribe On Youtube
3331. Find Subtree Sizes After Changes
Description
You are given a tree rooted at node 0 that consists of n nodes numbered from 0 to n - 1. The tree is represented by an array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.
You are also given a string s of length n, where s[i] is the character assigned to node i.
We make the following changes on the tree one time simultaneously for all nodes x from 1 to n - 1:
- Find the closest node
yto nodexsuch thatyis an ancestor ofx, ands[x] == s[y]. - If node
ydoes not exist, do nothing. - Otherwise, remove the edge between
xand its current parent and make nodeythe new parent ofxby adding an edge between them.
Return an array answer of size n where answer[i] is the size of the subtree rooted at node i in the final tree.
Example 1:
Input: parent = [-1,0,0,1,1,1], s = "abaabc"
Output: [6,3,1,1,1,1]
Explanation:
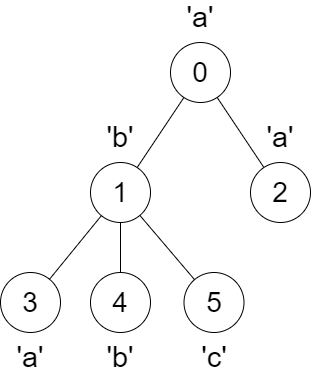
The parent of node 3 will change from node 1 to node 0.
Example 2:
Input: parent = [-1,0,4,0,1], s = "abbba"
Output: [5,2,1,1,1]
Explanation:
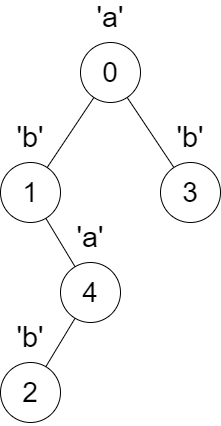
The following changes will happen at the same time:
- The parent of node 4 will change from node 1 to node 0.
- The parent of node 2 will change from node 4 to node 1.
Constraints:
n == parent.length == s.length1 <= n <= 1050 <= parent[i] <= n - 1for alli >= 1.parent[0] == -1parentrepresents a valid tree.sconsists only of lowercase English letters.
Solutions
Solution 1
-
class Solution { private List<Integer>[] g; private List<Integer>[] d; private char[] s; private int[] ans; public int[] findSubtreeSizes(int[] parent, String s) { int n = s.length(); g = new List[n]; d = new List[26]; this.s = s.toCharArray(); Arrays.setAll(g, k -> new ArrayList<>()); Arrays.setAll(d, k -> new ArrayList<>()); for (int i = 1; i < n; ++i) { g[parent[i]].add(i); } ans = new int[n]; dfs(0, -1); return ans; } private void dfs(int i, int fa) { ans[i] = 1; int idx = s[i] - 'a'; d[idx].add(i); for (int j : g[i]) { dfs(j, i); } int k = d[idx].size() > 1 ? d[idx].get(d[idx].size() - 2) : fa; if (k >= 0) { ans[k] += ans[i]; } d[idx].remove(d[idx].size() - 1); } } -
class Solution { public: vector<int> findSubtreeSizes(vector<int>& parent, string s) { int n = s.size(); vector<int> g[n]; vector<int> d[26]; for (int i = 1; i < n; ++i) { g[parent[i]].push_back(i); } vector<int> ans(n); auto dfs = [&](auto&& dfs, int i, int fa) -> void { ans[i] = 1; int idx = s[i] - 'a'; d[idx].push_back(i); for (int j : g[i]) { dfs(dfs, j, i); } int k = d[idx].size() > 1 ? d[idx][d[idx].size() - 2] : fa; if (k >= 0) { ans[k] += ans[i]; } d[idx].pop_back(); }; dfs(dfs, 0, -1); return ans; } }; -
class Solution: def findSubtreeSizes(self, parent: List[int], s: str) -> List[int]: def dfs(i: int, fa: int): ans[i] = 1 d[s[i]].append(i) for j in g[i]: dfs(j, i) k = fa if len(d[s[i]]) > 1: k = d[s[i]][-2] if k != -1: ans[k] += ans[i] d[s[i]].pop() n = len(s) g = [[] for _ in range(n)] for i in range(1, n): g[parent[i]].append(i) d = defaultdict(list) ans = [0] * n dfs(0, -1) return ans -
func findSubtreeSizes(parent []int, s string) []int { n := len(s) g := make([][]int, n) for i := 1; i < n; i++ { g[parent[i]] = append(g[parent[i]], i) } d := [26][]int{} ans := make([]int, n) var dfs func(int, int) dfs = func(i, fa int) { ans[i] = 1 idx := int(s[i] - 'a') d[idx] = append(d[idx], i) for _, j := range g[i] { dfs(j, i) } k := fa if len(d[idx]) > 1 { k = d[idx][len(d[idx])-2] } if k != -1 { ans[k] += ans[i] } d[idx] = d[idx][:len(d[idx])-1] } dfs(0, -1) return ans } -
function findSubtreeSizes(parent: number[], s: string): number[] { const n = parent.length; const g: number[][] = Array.from({ length: n }, () => []); const d: number[][] = Array.from({ length: 26 }, () => []); for (let i = 1; i < n; ++i) { g[parent[i]].push(i); } const ans: number[] = Array(n).fill(1); const dfs = (i: number, fa: number): void => { const idx = s.charCodeAt(i) - 97; d[idx].push(i); for (const j of g[i]) { dfs(j, i); } const k = d[idx].length > 1 ? d[idx].at(-2)! : fa; if (k >= 0) { ans[k] += ans[i]; } d[idx].pop(); }; dfs(0, -1); return ans; }