3327. Check if DFS Strings Are Palindromes

Description

You are given a tree rooted at node 0, consisting of n nodes numbered from 0 to n - 1. The tree is represented by an array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.

You are also given a string s of length n, where s[i] is the character assigned to node i.

Consider an empty string dfsStr, and define a recursive function dfs(int x) that takes a node x as a parameter and performs the following steps in order:

Iterate over each child y of x in increasing order of their numbers, and call dfs(y).
Add the character s[x] to the end of the string dfsStr.

Note that dfsStr is shared across all recursive calls of dfs.

You need to find a boolean array answer of size n, where for each index i from 0 to n - 1, you do the following:

Empty the string dfsStr and call dfs(i).
If the resulting string dfsStr is a palindrome, then set answer[i] to true. Otherwise, set answer[i] to false.

Return the array answer.

Example 1:

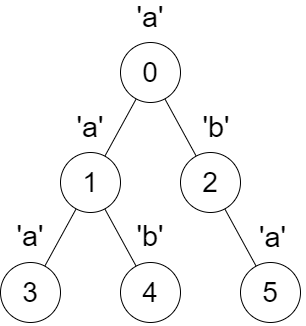
Input: parent = [-1,0,0,1,1,2], s = "aababa"

Output: [true,true,false,true,true,true]

Explanation:

Calling dfs(0) results in the string dfsStr = "abaaba", which is a palindrome.
Calling dfs(1) results in the string dfsStr = "aba", which is a palindrome.
Calling dfs(2) results in the string dfsStr = "ab", which is not a palindrome.
Calling dfs(3) results in the string dfsStr = "a", which is a palindrome.
Calling dfs(4) results in the string dfsStr = "b", which is a palindrome.
Calling dfs(5) results in the string dfsStr = "a", which is a palindrome.

Example 2:

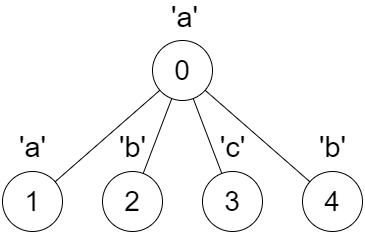
Input: parent = [-1,0,0,0,0], s = "aabcb"

Output: [true,true,true,true,true]

Explanation:

Every call on dfs(x) results in a palindrome string.

Constraints:

n == parent.length == s.length
1 <= n <= 10⁵
0 <= parent[i] <= n - 1 for all i >= 1.
parent[0] == -1
parent represents a valid tree.
s consists only of lowercase English letters.

Solutions

Solution 1: DFS + String Hashing

We can use Depth-First Search (DFS) to traverse the tree and compute the entire $\textit{dfsStr}$, while also determining the interval $[l, r]$ for each node.

Then, we use string hashing to compute the hash values of both $\textit{dfsStr}$ and the reverse of $\textit{dfsStr}$ to check if it is a palindrome.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the length of the string $s$.

class Hashing {
    private final long[] p;
    private final long[] h;
    private final long mod;

    public Hashing(String word, long base, int mod) {
        int n = word.length();
        p = new long[n + 1];
        h = new long[n + 1];
        p[0] = 1;
        this.mod = mod;
        for (int i = 1; i <= n; i++) {
            p[i] = p[i - 1] * base % mod;
            h[i] = (h[i - 1] * base + word.charAt(i - 1)) % mod;
        }
    }

    public long query(int l, int r) {
        return (h[r] - h[l - 1] * p[r - l + 1] % mod + mod) % mod;
    }
}

class Solution {
    private char[] s;
    private int[][] pos;
    private List<Integer>[] g;
    private StringBuilder dfsStr = new StringBuilder();

    public boolean[] findAnswer(int[] parent, String s) {
        this.s = s.toCharArray();
        int n = s.length();
        g = new List[n];
        pos = new int[n][0];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (int i = 1; i < n; ++i) {
            g[parent[i]].add(i);
        }
        dfs(0);
        final int base = 13331;
        final int mod = 998244353;
        Hashing h1 = new Hashing(dfsStr.toString(), base, mod);
        Hashing h2 = new Hashing(new StringBuilder(dfsStr).reverse().toString(), base, mod);
        boolean[] ans = new boolean[n];
        for (int i = 0; i < n; ++i) {
            int l = pos[i][0], r = pos[i][1];
            int k = r - l + 1;
            long v1 = h1.query(l, l + k / 2 - 1);
            long v2 = h2.query(n + 1 - r, n + 1 - r + k / 2 - 1);
            ans[i] = v1 == v2;
        }
        return ans;
    }

    private void dfs(int i) {
        int l = dfsStr.length() + 1;
        for (int j : g[i]) {
            dfs(j);
        }
        dfsStr.append(s[i]);
        int r = dfsStr.length();
        pos[i] = new int[] {l, r};
    }
}

class Hashing {
private:
    vector<long long> p;
    vector<long long> h;
    long long mod;

public:
    Hashing(string word, long long base, int mod) {
        int n = word.size();
        p.resize(n + 1);
        h.resize(n + 1);
        p[0] = 1;
        this->mod = mod;
        for (int i = 1; i <= n; i++) {
            p[i] = (p[i - 1] * base) % mod;
            h[i] = (h[i - 1] * base + word[i - 1] - 'a') % mod;
        }
    }

    long long query(int l, int r) {
        return (h[r] - h[l - 1] * p[r - l + 1] % mod + mod) % mod;
    }
};

class Solution {
public:
    vector<bool> findAnswer(vector<int>& parent, string s) {
        int n = s.size();
        vector<int> g[n];
        for (int i = 1; i < n; ++i) {
            g[parent[i]].push_back(i);
        }
        string dfsStr;
        vector<pair<int, int>> pos(n);
        auto dfs = [&](auto&& dfs, int i) -> void {
            int l = dfsStr.size() + 1;
            for (int j : g[i]) {
                dfs(dfs, j);
            }
            dfsStr.push_back(s[i]);
            int r = dfsStr.size();
            pos[i] = {l, r};
        };
        dfs(dfs, 0);

        const int base = 13331;
        const int mod = 998244353;
        Hashing h1(dfsStr, base, mod);
        reverse(dfsStr.begin(), dfsStr.end());
        Hashing h2(dfsStr, base, mod);
        vector<bool> ans(n);
        for (int i = 0; i < n; ++i) {
            auto [l, r] = pos[i];
            int k = r - l + 1;
            long long v1 = h1.query(l, l + k / 2 - 1);
            long long v2 = h2.query(n - r + 1, n - r + 1 + k / 2 - 1);
            ans[i] = v1 == v2;
        }
        return ans;
    }
};

class Hashing:
    __slots__ = ["mod", "h", "p"]

    def __init__(self, s: List[str], base: int, mod: int):
        self.mod = mod
        self.h = [0] * (len(s) + 1)
        self.p = [1] * (len(s) + 1)
        for i in range(1, len(s) + 1):
            self.h[i] = (self.h[i - 1] * base + ord(s[i - 1])) % mod
            self.p[i] = (self.p[i - 1] * base) % mod

    def query(self, l: int, r: int) -> int:
        return (self.h[r] - self.h[l - 1] * self.p[r - l + 1]) % self.mod


class Solution:
    def findAnswer(self, parent: List[int], s: str) -> List[bool]:
        def dfs(i: int):
            l = len(dfsStr) + 1
            for j in g[i]:
                dfs(j)
            dfsStr.append(s[i])
            r = len(dfsStr)
            pos[i] = (l, r)

        n = len(s)
        g = [[] for _ in range(n)]
        for i in range(1, n):
            g[parent[i]].append(i)
        dfsStr = []
        pos = {}
        dfs(0)

        base, mod = 13331, 998244353
        h1 = Hashing(dfsStr, base, mod)
        h2 = Hashing(dfsStr[::-1], base, mod)
        ans = []
        for i in range(n):
            l, r = pos[i]
            k = r - l + 1
            v1 = h1.query(l, l + k // 2 - 1)
            v2 = h2.query(n - r + 1, n - r + 1 + k // 2 - 1)
            ans.append(v1 == v2)
        return ans

type Hashing struct {
	p   []int64
	h   []int64
	mod int64
}

func NewHashing(word string, base, mod int64) *Hashing {
	n := len(word)
	p := make([]int64, n+1)
	h := make([]int64, n+1)
	p[0] = 1
	for i := 1; i <= n; i++ {
		p[i] = p[i-1] * base % mod
		h[i] = (h[i-1]*base + int64(word[i-1])) % mod
	}
	return &Hashing{p, h, mod}
}

func (hs *Hashing) query(l, r int) int64 {
	return (hs.h[r] - hs.h[l-1]*hs.p[r-l+1]%hs.mod + hs.mod) % hs.mod
}

func findAnswer(parent []int, s string) (ans []bool) {
	n := len(s)
	g := make([][]int, n)
	for i := 1; i < n; i++ {
		g[parent[i]] = append(g[parent[i]], i)
	}
	dfsStr := []byte{}
	pos := make([][2]int, n)
	var dfs func(int)
	dfs = func(i int) {
		l := len(dfsStr) + 1
		for _, j := range g[i] {
			dfs(j)
		}
		dfsStr = append(dfsStr, s[i])
		r := len(dfsStr)
		pos[i] = [2]int{l, r}
	}

	const base = 13331
	const mod = 998244353
	dfs(0)
	h1 := NewHashing(string(dfsStr), base, mod)
	for i, j := 0, len(dfsStr)-1; i < j; i, j = i+1, j-1 {
		dfsStr[i], dfsStr[j] = dfsStr[j], dfsStr[i]
	}
	h2 := NewHashing(string(dfsStr), base, mod)
	for i := 0; i < n; i++ {
		l, r := pos[i][0], pos[i][1]
		k := r - l + 1
		v1 := h1.query(l, l+k/2-1)
		v2 := h2.query(n-r+1, n-r+1+k/2-1)
		ans = append(ans, v1 == v2)
	}
	return
}

3327 - Check if DFS Strings Are Palindromes

3327. Check if DFS Strings Are Palindromes

Description

Solutions

Solution 1: DFS + String Hashing

All Problems

All Solutions

Welcome to Subscribe On Youtube

3327. Check if DFS Strings Are Palindromes

Description

Solutions

Solution 1: DFS + String Hashing

All Problems

All Solutions