Welcome to Subscribe On Youtube

3310. Remove Methods From Project

Description

You are maintaining a project that has n methods numbered from 0 to n - 1.

You are given two integers n and k, and a 2D integer array invocations, where invocations[i] = [ai, bi] indicates that method ai invokes method bi.

There is a known bug in method k. Method k, along with any method invoked by it, either directly or indirectly, are considered suspicious and we aim to remove them.

A group of methods can only be removed if no method outside the group invokes any methods within it.

Return an array containing all the remaining methods after removing all the suspicious methods. You may return the answer in any order. If it is not possible to remove all the suspicious methods, none should be removed.

 

Example 1:

Input: n = 4, k = 1, invocations = [[1,2],[0,1],[3,2]]

Output: [0,1,2,3]

Explanation:

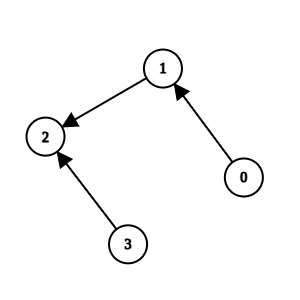
Method 2 and method 1 are suspicious, but they are directly invoked by methods 3 and 0, which are not suspicious. We return all elements without removing anything.

Example 2:

Input: n = 5, k = 0, invocations = [[1,2],[0,2],[0,1],[3,4]]

Output: [3,4]

Explanation:

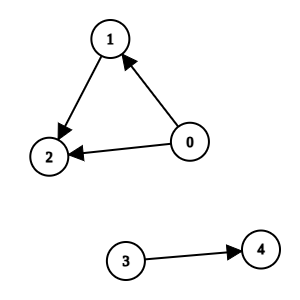
Methods 0, 1, and 2 are suspicious and they are not directly invoked by any other method. We can remove them.

Example 3:

Input: n = 3, k = 2, invocations = [[1,2],[0,1],[2,0]]

Output: []

Explanation:

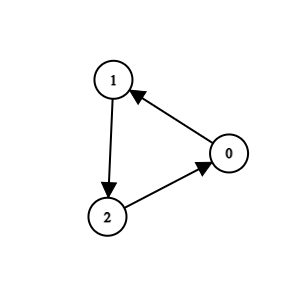
All methods are suspicious. We can remove them.

 

Constraints:

• 1 <= n <= 105
• 0 <= k <= n - 1
• 0 <= invocations.length <= 2 * 105
• invocations[i] == [ai, bi]
• 0 <= ai, bi <= n - 1
• ai != bi
• invocations[i] != invocations[j]

Solutions

Solution 1: Two DFS

We can start from $k$ and find all suspicious methods, recording them in the array $\textit{suspicious}$. Then, we traverse from $0$ to $n-1$, starting from all non-suspicious methods, and mark all reachable methods as non-suspicious. Finally, we return all non-suspicious methods.

The time complexity is $O(n + m)$, and the space complexity is $O(n + m)$. Here, $n$ and $m$ represent the number of methods and the number of call relationships, respectively.

Solution 2: Two Explicit-Stack Passes

Thinking

Methods reachable from $k$ along call edges are suspicious, yet we must not remove a node that a clean method still invokes. With $n \le 10^5$, linear traversals are enough.

Recursing from $k$ into each callee reaches depth $n$ on a chain and overflows the call stack. Both the suspicious set and the later cleared set depend only on reachability, so neighbor order does not matter.

Both passes therefore use an explicit stack. The first marks the directed closure of $k$, marking a node when it is pushed. The second starts from every still-unmarked node and, along undirected edges, clears any node a clean method can reach. Only nodes that remain marked are removed; the rest form the answer.

An explicit stack starts from $k$ and follows directed call edges, recording suspicious methods in $\textit{suspicious}$ and marking a node when it is pushed. We then scan from $0$ to $n - 1$. From each non-suspicious method, another explicit stack follows undirected edges and marks every reachable method as non-suspicious. Finally, we return all non-suspicious methods.

The time complexity is $O(n + m)$, and the space complexity is $O(n + m)$. Here, $n$ and $m$ represent the number of methods and the number of call relationships, respectively.

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      private boolean[] suspicious;
      private boolean[] vis;
      private List<Integer>[] f;
      private List<Integer>[] g;
  
      public List<Integer> remainingMethods(int n, int k, int[][] invocations) {
          suspicious = new boolean[n];
          vis = new boolean[n];
          f = new List[n];
          g = new List[n];
          Arrays.setAll(f, i -> new ArrayList<>());
          Arrays.setAll(g, i -> new ArrayList<>());
          for (var e : invocations) {
              int a = e[0], b = e[1];
              f[a].add(b);
              f[b].add(a);
              g[a].add(b);
          }
          dfs(k);
          for (int i = 0; i < n; ++i) {
              if (!suspicious[i] && !vis[i]) {
                  dfs2(i);
              }
          }
          List<Integer> ans = new ArrayList<>();
          for (int i = 0; i < n; ++i) {
              if (!suspicious[i]) {
                  ans.add(i);
              }
          }
          return ans;
      }
  
      private void dfs(int i) {
          suspicious[i] = true;
          for (int j : g[i]) {
              if (!suspicious[j]) {
                  dfs(j);
              }
          }
      }
  
      private void dfs2(int i) {
          vis[i] = true;
          for (int j : f[i]) {
              if (!vis[j]) {
                  suspicious[j] = false;
                  dfs2(j);
              }
          }
      }
  }
  
  
  
  // Solution 2
  class Solution {
      public List<Integer> remainingMethods(int n, int k, int[][] invocations) {
          List<Integer>[] f = new List[n];
          List<Integer>[] g = new List[n];
          Arrays.setAll(f, i -> new ArrayList<>());
          Arrays.setAll(g, i -> new ArrayList<>());
          for (var e : invocations) {
              int a = e[0], b = e[1];
              f[a].add(b);
              f[b].add(a);
              g[a].add(b);
          }
          boolean[] suspicious = new boolean[n];
          suspicious[k] = true;
          Deque<Integer> stk = new ArrayDeque<>();
          stk.push(k);
          while (!stk.isEmpty()) {
              int i = stk.pop();
              for (int j : g[i]) {
                  if (!suspicious[j]) {
                      suspicious[j] = true;
                      stk.push(j);
                  }
              }
          }
          boolean[] vis = new boolean[n];
          for (int i = 0; i < n; ++i) {
              if (suspicious[i] || vis[i]) {
                  continue;
              }
              vis[i] = true;
              stk.push(i);
              while (!stk.isEmpty()) {
                  int u = stk.pop();
                  for (int j : f[u]) {
                      if (!vis[j]) {
                          suspicious[j] = false;
                          vis[j] = true;
                          stk.push(j);
                      }
                  }
              }
          }
          List<Integer> ans = new ArrayList<>();
          for (int i = 0; i < n; ++i) {
              if (!suspicious[i]) {
                  ans.add(i);
              }
          }
          return ans;
      }
  }
  
  

• class Solution {
  public:
      vector<int> remainingMethods(int n, int k, vector<vector<int>>& invocations) {
          vector<bool> suspicious(n);
          vector<bool> vis(n);
          vector<int> f[n];
          vector<int> g[n];
          for (const auto& e : invocations) {
              int a = e[0], b = e[1];
              f[a].push_back(b);
              f[b].push_back(a);
              g[a].push_back(b);
          }
          auto dfs = [&](auto&& dfs, int i) -> void {
              suspicious[i] = true;
              for (int j : g[i]) {
                  if (!suspicious[j]) {
                      dfs(dfs, j);
                  }
              }
          };
          dfs(dfs, k);
          auto dfs2 = [&](auto&& dfs2, int i) -> void {
              vis[i] = true;
              for (int j : f[i]) {
                  if (!vis[j]) {
                      suspicious[j] = false;
                      dfs2(dfs2, j);
                  }
              }
          };
          for (int i = 0; i < n; ++i) {
              if (!suspicious[i] && !vis[i]) {
                  dfs2(dfs2, i);
              }
          }
          vector<int> ans;
          for (int i = 0; i < n; ++i) {
              if (!suspicious[i]) {
                  ans.push_back(i);
              }
          }
          return ans;
      }
  };
  
  
  
  // Solution 2
  class Solution {
  public:
      vector<int> remainingMethods(int n, int k, vector<vector<int>>& invocations) {
          vector<vector<int>> f(n), g(n);
          for (const auto& e : invocations) {
              int a = e[0], b = e[1];
              f[a].push_back(b);
              f[b].push_back(a);
              g[a].push_back(b);
          }
          vector<char> suspicious(n), vis(n);
          suspicious[k] = 1;
          vector<int> stk{k};
          while (!stk.empty()) {
              int i = stk.back();
              stk.pop_back();
              for (int j : g[i]) {
                  if (!suspicious[j]) {
                      suspicious[j] = 1;
                      stk.push_back(j);
                  }
              }
          }
          for (int i = 0; i < n; ++i) {
              if (suspicious[i] || vis[i]) {
                  continue;
              }
              vis[i] = 1;
              stk.push_back(i);
              while (!stk.empty()) {
                  int u = stk.back();
                  stk.pop_back();
                  for (int j : f[u]) {
                      if (!vis[j]) {
                          suspicious[j] = 0;
                          vis[j] = 1;
                          stk.push_back(j);
                      }
                  }
              }
          }
          vector<int> ans;
          for (int i = 0; i < n; ++i) {
              if (!suspicious[i]) {
                  ans.push_back(i);
              }
          }
          return ans;
      }
  };
  
  

• class Solution:
      def remainingMethods(
          self, n: int, k: int, invocations: List[List[int]]
      ) -> List[int]:
          def dfs(i: int):
              suspicious[i] = True
              for j in g[i]:
                  if not suspicious[j]:
                      dfs(j)
  
          def dfs2(i: int):
              vis[i] = True
              for j in f[i]:
                  if not vis[j]:
                      suspicious[j] = False
                      dfs2(j)
  
          f = [[] for _ in range(n)]
          g = [[] for _ in range(n)]
          for a, b in invocations:
              f[a].append(b)
              f[b].append(a)
              g[a].append(b)
          suspicious = [False] * n
          dfs(k)
  
          vis = [False] * n
          ans = []
          for i in range(n):
              if not suspicious[i] and not vis[i]:
                  dfs2(i)
          return [i for i in range(n) if not suspicious[i]]
  
  
  
  # Solution 2
  class Solution:
      def remainingMethods(
          self, n: int, k: int, invocations: List[List[int]]
      ) -> List[int]:
          f = [[] for _ in range(n)]
          g = [[] for _ in range(n)]
          for a, b in invocations:
              f[a].append(b)
              f[b].append(a)
              g[a].append(b)
          suspicious = [False] * n
          suspicious[k] = True
          stk = [k]
          while stk:
              i = stk.pop()
              for j in g[i]:
                  if not suspicious[j]:
                      suspicious[j] = True
                      stk.append(j)
          vis = [False] * n
          for i in range(n):
              if suspicious[i] or vis[i]:
                  continue
              vis[i] = True
              stk = [i]
              while stk:
                  u = stk.pop()
                  for j in f[u]:
                      if not vis[j]:
                          suspicious[j] = False
                          vis[j] = True
                          stk.append(j)
          return [i for i in range(n) if not suspicious[i]]
  
  

• func remainingMethods(n int, k int, invocations [][]int) []int {
  	suspicious := make([]bool, n)
  	vis := make([]bool, n)
  	f := make([][]int, n)
  	g := make([][]int, n)
  
  	for _, e := range invocations {
  		a, b := e[0], e[1]
  		f[a] = append(f[a], b)
  		f[b] = append(f[b], a)
  		g[a] = append(g[a], b)
  	}
  
  	var dfs func(int)
  	dfs = func(i int) {
  		suspicious[i] = true
  		for _, j := range g[i] {
  			if !suspicious[j] {
  				dfs(j)
  			}
  		}
  	}
  
  	dfs(k)
  
  	var dfs2 func(int)
  	dfs2 = func(i int) {
  		vis[i] = true
  		for _, j := range f[i] {
  			if !vis[j] {
  				suspicious[j] = false
  				dfs2(j)
  			}
  		}
  	}
  
  	for i := 0; i < n; i++ {
  		if !suspicious[i] && !vis[i] {
  			dfs2(i)
  		}
  	}
  
  	var ans []int
  	for i := 0; i < n; i++ {
  		if !suspicious[i] {
  			ans = append(ans, i)
  		}
  	}
  
  	return ans
  }
  
  
  
  // Solution 2
  func remainingMethods(n int, k int, invocations [][]int) []int {
  	suspicious := make([]bool, n)
  	vis := make([]bool, n)
  	f := make([][]int, n)
  	g := make([][]int, n)
  	for _, e := range invocations {
  		a, b := e[0], e[1]
  		f[a] = append(f[a], b)
  		f[b] = append(f[b], a)
  		g[a] = append(g[a], b)
  	}
  	suspicious[k] = true
  	stk := []int{k}
  	for len(stk) > 0 {
  		i := stk[len(stk)-1]
  		stk = stk[:len(stk)-1]
  		for _, j := range g[i] {
  			if !suspicious[j] {
  				suspicious[j] = true
  				stk = append(stk, j)
  			}
  		}
  	}
  	for i := 0; i < n; i++ {
  		if suspicious[i] || vis[i] {
  			continue
  		}
  		vis[i] = true
  		stk = []int{i}
  		for len(stk) > 0 {
  			u := stk[len(stk)-1]
  			stk = stk[:len(stk)-1]
  			for _, j := range f[u] {
  				if !vis[j] {
  					suspicious[j] = false
  					vis[j] = true
  					stk = append(stk, j)
  				}
  			}
  		}
  	}
  	var ans []int
  	for i := 0; i < n; i++ {
  		if !suspicious[i] {
  			ans = append(ans, i)
  		}
  	}
  	return ans
  }
  
  

• function remainingMethods(n: number, k: number, invocations: number[][]): number[] {
      const suspicious: boolean[] = Array(n).fill(false);
      const vis: boolean[] = Array(n).fill(false);
      const f: number[][] = Array.from({ length: n }, () => []);
      const g: number[][] = Array.from({ length: n }, () => []);
  
      for (const [a, b] of invocations) {
          f[a].push(b);
          f[b].push(a);
          g[a].push(b);
      }
  
      const dfs = (i: number) => {
          suspicious[i] = true;
          for (const j of g[i]) {
              if (!suspicious[j]) {
                  dfs(j);
              }
          }
      };
  
      dfs(k);
  
      const dfs2 = (i: number) => {
          vis[i] = true;
          for (const j of f[i]) {
              if (!vis[j]) {
                  suspicious[j] = false;
                  dfs2(j);
              }
          }
      };
  
      for (let i = 0; i < n; i++) {
          if (!suspicious[i] && !vis[i]) {
              dfs2(i);
          }
      }
  
      return Array.from({ length: n }, (_, i) => i).filter(i => !suspicious[i]);
  }
  
  
  
  // Solution 2
  function remainingMethods(n: number, k: number, invocations: number[][]): number[] {
      const suspicious: boolean[] = Array(n).fill(false);
      const vis: boolean[] = Array(n).fill(false);
      const f: number[][] = Array.from({ length: n }, () => []);
      const g: number[][] = Array.from({ length: n }, () => []);
  
      for (const [a, b] of invocations) {
          f[a].push(b);
          f[b].push(a);
          g[a].push(b);
      }
  
      suspicious[k] = true;
      let stk: number[] = [k];
      while (stk.length) {
          const i = stk.pop()!;
          for (const j of g[i]) {
              if (!suspicious[j]) {
                  suspicious[j] = true;
                  stk.push(j);
              }
          }
      }
  
      for (let i = 0; i < n; i++) {
          if (suspicious[i] || vis[i]) {
              continue;
          }
          vis[i] = true;
          stk = [i];
          while (stk.length) {
              const u = stk.pop()!;
              for (const j of f[u]) {
                  if (!vis[j]) {
                      suspicious[j] = false;
                      vis[j] = true;
                      stk.push(j);
                  }
              }
          }
      }
  
      return Array.from({ length: n }, (_, i) => i).filter(i => !suspicious[i]);
  }
  
  

All Problems

All Solutions