Welcome to Subscribe On Youtube
3249. Count the Number of Good Nodes
Description
There is an undirected tree with n nodes labeled from 0 to n - 1, and rooted at node 0. You are given a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
A node is good if all the subtrees rooted at its children have the same size.
Return the number of good nodes in the given tree.
A subtree of treeName is a tree consisting of a node in treeName and all of its descendants.
Example 1:
Input: edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
Output: 7
Explanation:
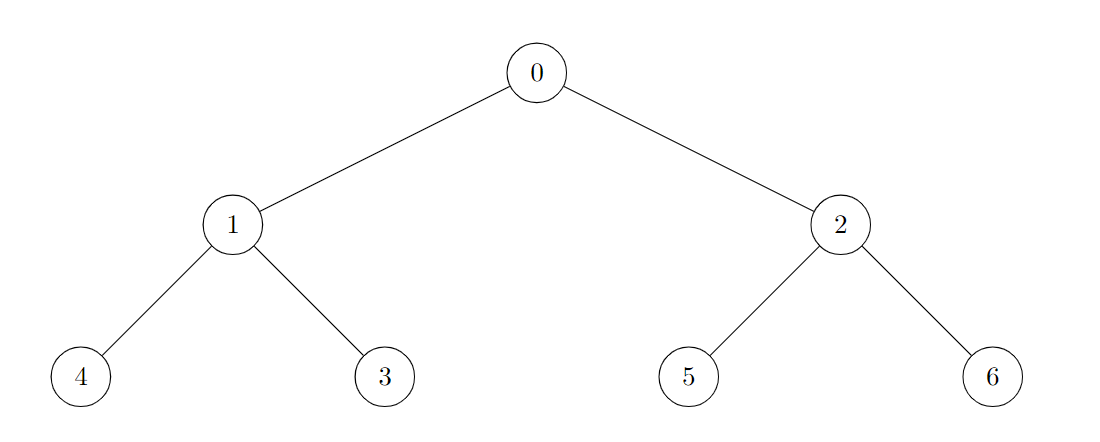
All of the nodes of the given tree are good.
Example 2:
Input: edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]
Output: 6
Explanation:
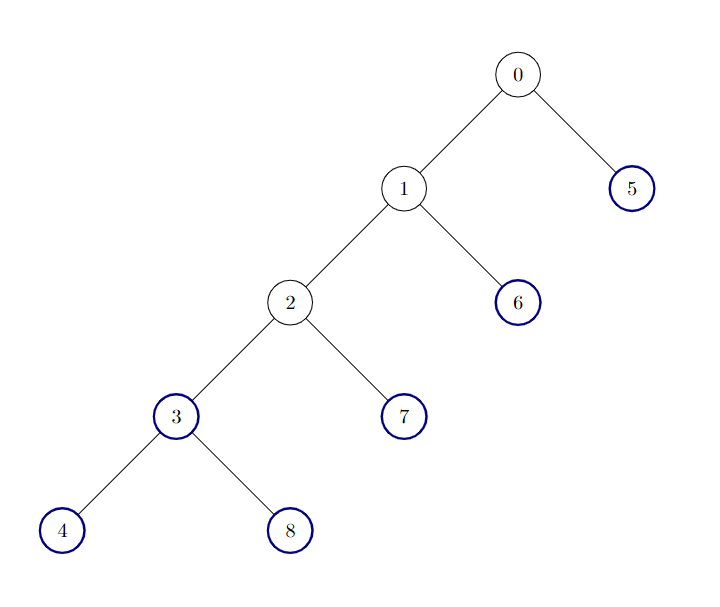
There are 6 good nodes in the given tree. They are colored in the image above.
Example 3:
Input: edges = [[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]
Output: 12
Explanation:
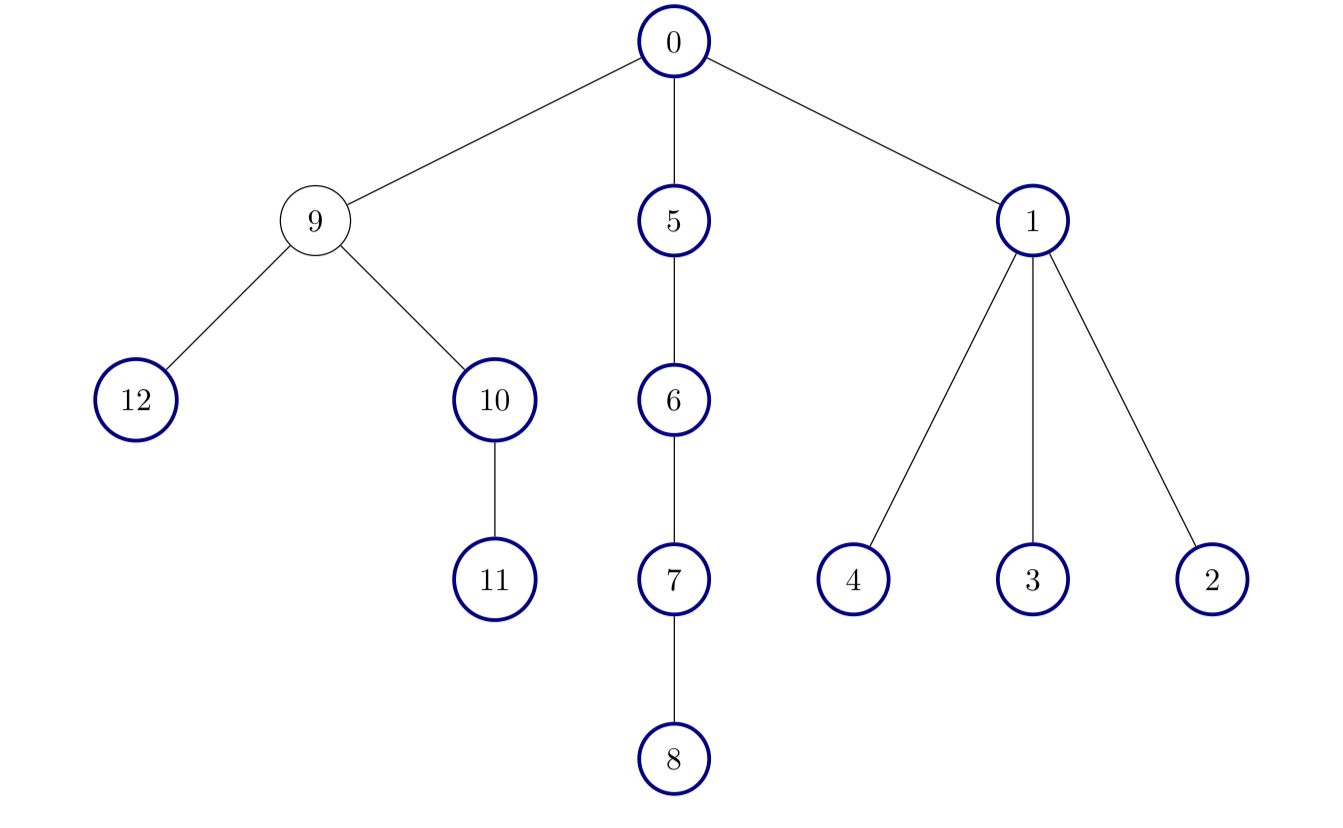
All nodes except node 9 are good.
Constraints:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < n- The input is generated such that
edgesrepresents a valid tree.
Solutions
Solution 1: DFS
First, we construct the adjacency list $\textit{g}$ of the tree based on the given edges $\textit{edges}$, where $\textit{g}[a]$ represents all the neighboring nodes of node $a$.
Next, we design a function $\textit{dfs}(a, \textit{fa})$ to calculate the number of nodes in the subtree rooted at node $a$ and to accumulate the count of good nodes. Here, $\textit{fa}$ represents the parent node of node $a$.
The execution process of the function $\textit{dfs}(a, \textit{fa})$ is as follows:
- Initialize variables $\textit{pre} = -1$, $\textit{cnt} = 1$, $\textit{ok} = 1$, representing the number of nodes in a subtree of node $a$, the total number of nodes in all subtrees of node $a$, and whether node $a$ is a good node, respectively.
- Traverse all neighboring nodes $b$ of node $a$. If $b$ is not equal to $\textit{fa}$, recursively call $\textit{dfs}(b, a)$, with the return value being $\textit{cur}$, and add $\textit{cur}$ to $\textit{cnt}$. If $\textit{pre} < 0$, assign $\textit{cur}$ to $\textit{pre}$; otherwise, if $\textit{pre}$ is not equal to $\textit{cur}$, it means the number of nodes in different subtrees of node $a$ is different, and set $\textit{ok}$ to $0$.
- Finally, add $\textit{ok}$ to the answer and return $\textit{cnt}$.
In the main function, we call $\textit{dfs}(0, -1)$ and return the final answer.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ represents the number of nodes.
-
class Solution { private int ans; private List<Integer>[] g; public int countGoodNodes(int[][] edges) { int n = edges.length + 1; g = new List[n]; Arrays.setAll(g, k -> new ArrayList<>()); for (var e : edges) { int a = e[0], b = e[1]; g[a].add(b); g[b].add(a); } dfs(0, -1); return ans; } private int dfs(int a, int fa) { int pre = -1, cnt = 1, ok = 1; for (int b : g[a]) { if (b != fa) { int cur = dfs(b, a); cnt += cur; if (pre < 0) { pre = cur; } else if (pre != cur) { ok = 0; } } } ans += ok; return cnt; } } -
class Solution { public: int countGoodNodes(vector<vector<int>>& edges) { int n = edges.size() + 1; vector<int> g[n]; for (const auto& e : edges) { int a = e[0], b = e[1]; g[a].push_back(b); g[b].push_back(a); } int ans = 0; auto dfs = [&](auto&& dfs, int a, int fa) -> int { int pre = -1, cnt = 1, ok = 1; for (int b : g[a]) { if (b != fa) { int cur = dfs(dfs, b, a); cnt += cur; if (pre < 0) { pre = cur; } else if (pre != cur) { ok = 0; } } } ans += ok; return cnt; }; dfs(dfs, 0, -1); return ans; } }; -
class Solution: def countGoodNodes(self, edges: List[List[int]]) -> int: def dfs(a: int, fa: int) -> int: pre = -1 cnt = ok = 1 for b in g[a]: if b != fa: cur = dfs(b, a) cnt += cur if pre < 0: pre = cur elif pre != cur: ok = 0 nonlocal ans ans += ok return cnt g = defaultdict(list) for a, b in edges: g[a].append(b) g[b].append(a) ans = 0 dfs(0, -1) return ans -
func countGoodNodes(edges [][]int) (ans int) { n := len(edges) + 1 g := make([][]int, n) for _, e := range edges { a, b := e[0], e[1] g[a] = append(g[a], b) g[b] = append(g[b], a) } var dfs func(int, int) int dfs = func(a, fa int) int { pre, cnt, ok := -1, 1, 1 for _, b := range g[a] { if b != fa { cur := dfs(b, a) cnt += cur if pre < 0 { pre = cur } else if pre != cur { ok = 0 } } } ans += ok return cnt } dfs(0, -1) return } -
function countGoodNodes(edges: number[][]): number { const n = edges.length + 1; const g: number[][] = Array.from({ length: n }, () => []); for (const [a, b] of edges) { g[a].push(b); g[b].push(a); } let ans = 0; const dfs = (a: number, fa: number): number => { let [pre, cnt, ok] = [-1, 1, 1]; for (const b of g[a]) { if (b !== fa) { const cur = dfs(b, a); cnt += cur; if (pre < 0) { pre = cur; } else if (pre !== cur) { ok = 0; } } } ans += ok; return cnt; }; dfs(0, -1); return ans; }