Welcome to Subscribe On Youtube
3212. Count Submatrices With Equal Frequency of X and Y
Description
Given a 2D character matrix grid, where grid[i][j] is either 'X', 'Y', or '.', return the number of submatrices that contain:
grid[0][0]- an equal frequency of
'X'and'Y'. - at least one
'X'.
Example 1:
Input: grid = [["X","Y","."],["Y",".","."]]
Output: 3
Explanation:
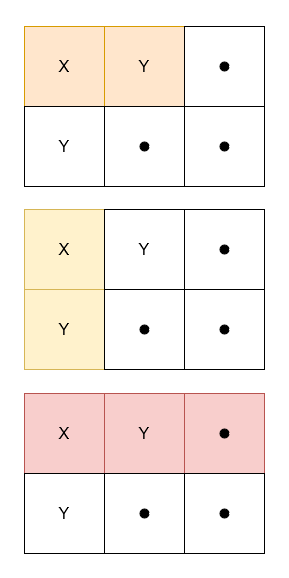
Example 2:
Input: grid = [["X","X"],["X","Y"]]
Output: 0
Explanation:
No submatrix has an equal frequency of 'X' and 'Y'.
Example 3:
Input: grid = [[".","."],[".","."]]
Output: 0
Explanation:
No submatrix has at least one 'X'.
Constraints:
1 <= grid.length, grid[i].length <= 1000grid[i][j]is either'X','Y', or'.'.
Solutions
Solution 1: 2D Prefix Sum
According to the problem description, we only need to calculate the prefix sums $s[i][j][0]$ and $s[i][j][1]$ for each position $(i, j)$, which represent the number of characters X and Y in the submatrix from $(0, 0)$ to $(i, j)$, respectively. If $s[i][j][0] > 0$ and $s[i][j][0] = s[i][j][1]$, it means the condition is met, and we increment the answer by one.
After traversing all positions, return the answer.
The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ represent the number of rows and columns of the matrix, respectively.
-
class Solution { public int numberOfSubmatrices(char[][] grid) { int m = grid.length, n = grid[0].length; int[][][] s = new int[m + 1][n + 1][2]; int ans = 0; for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { s[i][j][0] = s[i - 1][j][0] + s[i][j - 1][0] - s[i - 1][j - 1][0] + (grid[i - 1][j - 1] == 'X' ? 1 : 0); s[i][j][1] = s[i - 1][j][1] + s[i][j - 1][1] - s[i - 1][j - 1][1] + (grid[i - 1][j - 1] == 'Y' ? 1 : 0); if (s[i][j][0] > 0 && s[i][j][0] == s[i][j][1]) { ++ans; } } } return ans; } } -
class Solution { public: int numberOfSubmatrices(vector<vector<char>>& grid) { int m = grid.size(), n = grid[0].size(); vector<vector<vector<int>>> s(m + 1, vector<vector<int>>(n + 1, vector<int>(2))); int ans = 0; for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { s[i][j][0] = s[i - 1][j][0] + s[i][j - 1][0] - s[i - 1][j - 1][0] + (grid[i - 1][j - 1] == 'X' ? 1 : 0); s[i][j][1] = s[i - 1][j][1] + s[i][j - 1][1] - s[i - 1][j - 1][1] + (grid[i - 1][j - 1] == 'Y' ? 1 : 0); if (s[i][j][0] > 0 && s[i][j][0] == s[i][j][1]) { ++ans; } } } return ans; } }; -
class Solution: def numberOfSubmatrices(self, grid: List[List[str]]) -> int: m, n = len(grid), len(grid[0]) s = [[[0] * 2 for _ in range(n + 1)] for _ in range(m + 1)] ans = 0 for i, row in enumerate(grid, 1): for j, x in enumerate(row, 1): s[i][j][0] = s[i - 1][j][0] + s[i][j - 1][0] - s[i - 1][j - 1][0] s[i][j][1] = s[i - 1][j][1] + s[i][j - 1][1] - s[i - 1][j - 1][1] if x != ".": s[i][j][ord(x) & 1] += 1 if s[i][j][0] > 0 and s[i][j][0] == s[i][j][1]: ans += 1 return ans -
func numberOfSubmatrices(grid [][]byte) (ans int) { m, n := len(grid), len(grid[0]) s := make([][][]int, m+1) for i := range s { s[i] = make([][]int, n+1) for j := range s[i] { s[i][j] = make([]int, 2) } } for i := 1; i <= m; i++ { for j := 1; j <= n; j++ { s[i][j][0] = s[i-1][j][0] + s[i][j-1][0] - s[i-1][j-1][0] if grid[i-1][j-1] == 'X' { s[i][j][0]++ } s[i][j][1] = s[i-1][j][1] + s[i][j-1][1] - s[i-1][j-1][1] if grid[i-1][j-1] == 'Y' { s[i][j][1]++ } if s[i][j][0] > 0 && s[i][j][0] == s[i][j][1] { ans++ } } } return } -
function numberOfSubmatrices(grid: string[][]): number { const [m, n] = [grid.length, grid[0].length]; const s = Array.from({ length: m + 1 }, () => Array.from({ length: n + 1 }, () => [0, 0])); let ans = 0; for (let i = 1; i <= m; ++i) { for (let j = 1; j <= n; ++j) { s[i][j][0] = s[i - 1][j][0] + s[i][j - 1][0] - s[i - 1][j - 1][0] + (grid[i - 1][j - 1] === 'X' ? 1 : 0); s[i][j][1] = s[i - 1][j][1] + s[i][j - 1][1] - s[i - 1][j - 1][1] + (grid[i - 1][j - 1] === 'Y' ? 1 : 0); if (s[i][j][0] > 0 && s[i][j][0] === s[i][j][1]) { ++ans; } } } return ans; }