Welcome to Subscribe On Youtube

3206. Alternating Groups I

Description

There is a circle of red and blue tiles. You are given an array of integers colors. The color of tile i is represented by colors[i]:

• colors[i] == 0 means that tile i is red.
• colors[i] == 1 means that tile i is blue.

Every 3 contiguous tiles in the circle with alternating colors (the middle tile has a different color from its left and right tiles) is called an alternating group.

Return the number of alternating groups.

Note that since colors represents a circle, the first and the last tiles are considered to be next to each other.

 

Example 1:

Input: colors = [1,1,1]

Output: 0

Explanation:

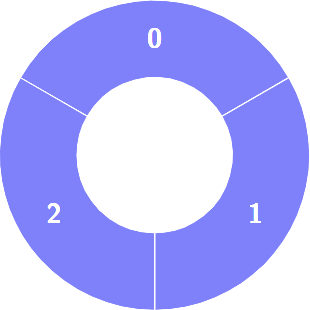
Example 2:

Input: colors = [0,1,0,0,1]

Output: 3

Explanation:

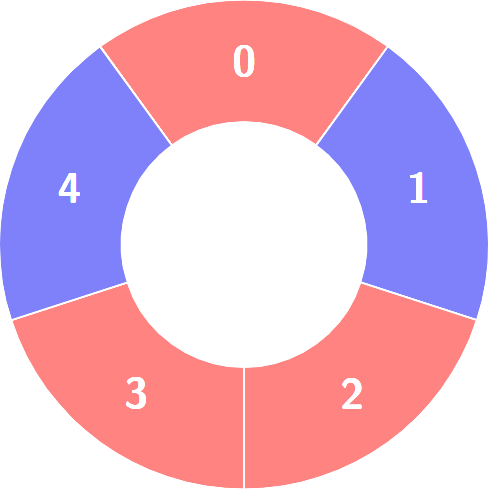
Alternating groups:

 

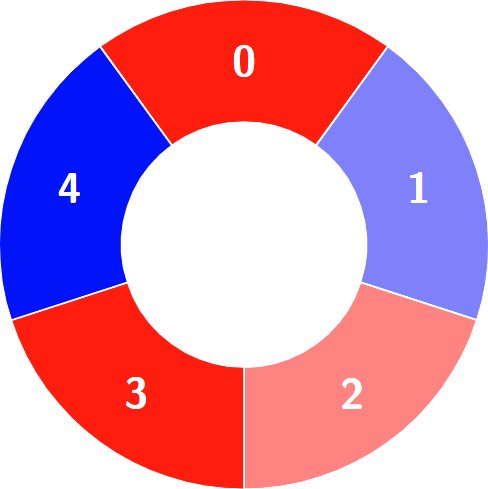
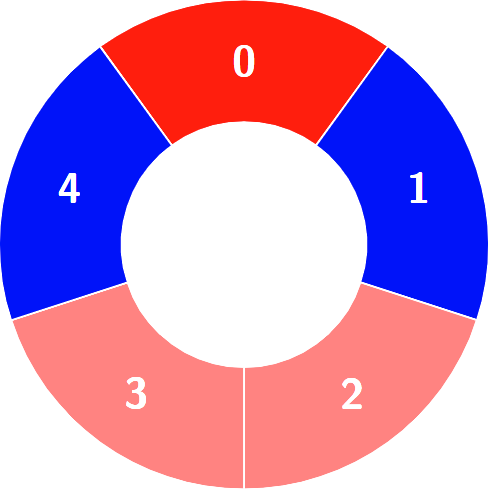
Constraints:

• 3 <= colors.length <= 100
• 0 <= colors[i] <= 1

Solutions

Solution 1: Single Pass

We set $k = 3$, indicating that the length of the alternating group is $3$.

For convenience, we can unfold the ring into an array of length $2n$ and then traverse this array from left to right. We use a variable $\textit{cnt}$ to record the current length of the alternating group. If we encounter the same color, we reset $\textit{cnt}$ to $1$; otherwise, we increment $\textit{cnt}$. If $\textit{cnt} \ge k$ and the current position $i$ is greater than or equal to $n$, then we have found an alternating group, and we increment the answer by one.

After the traversal, we return the answer.

The time complexity is $O(n)$, where $n$ is the length of the array $\textit{colors}$. The space complexity is $O(1)$.

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      public int numberOfAlternatingGroups(int[] colors) {
          int k = 3;
          int n = colors.length;
          int ans = 0, cnt = 0;
          for (int i = 0; i < n << 1; ++i) {
              if (i > 0 && colors[i % n] == colors[(i - 1) % n]) {
                  cnt = 1;
              } else {
                  ++cnt;
              }
              ans += i >= n && cnt >= k ? 1 : 0;
          }
          return ans;
      }
  }
  

• class Solution {
  public:
      int numberOfAlternatingGroups(vector<int>& colors) {
          int k = 3;
          int n = colors.size();
          int ans = 0, cnt = 0;
          for (int i = 0; i < n << 1; ++i) {
              if (i && colors[i % n] == colors[(i - 1) % n]) {
                  cnt = 1;
              } else {
                  ++cnt;
              }
              ans += i >= n && cnt >= k ? 1 : 0;
          }
          return ans;
      }
  };
  

• class Solution:
      def numberOfAlternatingGroups(self, colors: List[int]) -> int:
          k = 3
          n = len(colors)
          ans = cnt = 0
          for i in range(n << 1):
              if i and colors[i % n] == colors[(i - 1) % n]:
                  cnt = 1
              else:
                  cnt += 1
              ans += i >= n and cnt >= k
          return ans
  
  

• func numberOfAlternatingGroups(colors []int) (ans int) {
  	k := 3
  	n := len(colors)
  	cnt := 0
  	for i := 0; i < n<<1; i++ {
  		if i > 0 && colors[i%n] == colors[(i-1)%n] {
  			cnt = 1
  		} else {
  			cnt++
  		}
  		if i >= n && cnt >= k {
  			ans++
  		}
  	}
  	return
  }
  

• function numberOfAlternatingGroups(colors: number[]): number {
      const k = 3;
      const n = colors.length;
      let [ans, cnt] = [0, 0];
      for (let i = 0; i < n << 1; ++i) {
          if (i && colors[i % n] === colors[(i - 1) % n]) {
              cnt = 1;
          } else {
              ++cnt;
          }
          ans += i >= n && cnt >= k ? 1 : 0;
      }
      return ans;
  }
  
  

All Problems

All Solutions