Welcome to Subscribe On Youtube

3195. Find the Minimum Area to Cover All Ones I

Description

You are given a 2D binary array grid. Find a rectangle with horizontal and vertical sides with the smallest area, such that all the 1's in grid lie inside this rectangle.

Return the minimum possible area of the rectangle.

 

Example 1:

Input: grid = [[0,1,0],[1,0,1]]

Output: 6

Explanation:

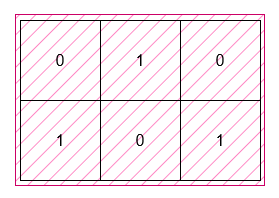
The smallest rectangle has a height of 2 and a width of 3, so it has an area of 2 * 3 = 6.

Example 2:

Input: grid = [[1,0],[0,0]]

Output: 1

Explanation:

The smallest rectangle has both height and width 1, so its area is 1 * 1 = 1.

 

Constraints:

  • 1 <= grid.length, grid[i].length <= 1000
  • grid[i][j] is either 0 or 1.
  • The input is generated such that there is at least one 1 in grid.

Solutions

Solution 1: Find Minimum and Maximum Boundaries

We can traverse grid, finding the minimum boundary of all 1s, denoted as $(x_1, y_1)$, and the maximum boundary, denoted as $(x_2, y_2)$. Then, the area of the minimum rectangle is $(x_2 - x_1 + 1) \times (y_2 - y_1 + 1)$.

The time complexity is $O(m \times n)$, where $m$ and $n$ are the number of rows and columns in grid, respectively. The space complexity is $O(1)$.

  • class Solution {
    public int minimumArea(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int x1 = m, y1 = n;
        int x2 = 0, y2 = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    x1 = Math.min(x1, i);
                    y1 = Math.min(y1, j);
                    x2 = Math.max(x2, i);
                    y2 = Math.max(y2, j);
                }
            }
        }
        return (x2 - x1 + 1) * (y2 - y1 + 1);
    }
}

  • class Solution {
public:
    int minimumArea(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int x1 = m, y1 = n;
        int x2 = 0, y2 = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    x1 = min(x1, i);
                    y1 = min(y1, j);
                    x2 = max(x2, i);
                    y2 = max(y2, j);
                }
            }
        }
        return (x2 - x1 + 1) * (y2 - y1 + 1);
    }
};

  • class Solution:
    def minimumArea(self, grid: List[List[int]]) -> int:
        x1 = y1 = inf
        x2 = y2 = -inf
        for i, row in enumerate(grid):
            for j, x in enumerate(row):
                if x == 1:
                    x1 = min(x1, i)
                    y1 = min(y1, j)
                    x2 = max(x2, i)
                    y2 = max(y2, j)
        return (x2 - x1 + 1) * (y2 - y1 + 1)


  • func minimumArea(grid [][]int) int {
	x1, y1 := len(grid), len(grid[0])
	x2, y2 := 0, 0
	for i, row := range grid {
		for j, x := range row {
			if x == 1 {
				x1, y1 = min(x1, i), min(y1, j)
				x2, y2 = max(x2, i), max(y2, j)
			}
		}
	}
	return (x2 - x1 + 1) * (y2 - y1 + 1)
}

  • function minimumArea(grid: number[][]): number {
    const [m, n] = [grid.length, grid[0].length];
    let [x1, y1] = [m, n];
    let [x2, y2] = [0, 0];
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (grid[i][j] === 1) {
                x1 = Math.min(x1, i);
                y1 = Math.min(y1, j);
                x2 = Math.max(x2, i);
                y2 = Math.max(y2, j);
            }
        }
    }
    return (x2 - x1 + 1) * (y2 - y1 + 1);
}

All Problems

All Solutions