Welcome to Subscribe On Youtube
3160. Find the Number of Distinct Colors Among the Balls
Description
You are given an integer limit and a 2D array queries of size n x 2.
There are limit + 1 balls with distinct labels in the range [0, limit]. Initially, all balls are uncolored. For every query in queries that is of the form [x, y], you mark ball x with the color y. After each query, you need to find the number of distinct colors among the balls.
Return an array result of length n, where result[i] denotes the number of distinct colors after ith query.
Note that when answering a query, lack of a color will not be considered as a color.
Example 1:
Input: limit = 4, queries = [[1,4],[2,5],[1,3],[3,4]]
Output: [1,2,2,3]
Explanation:
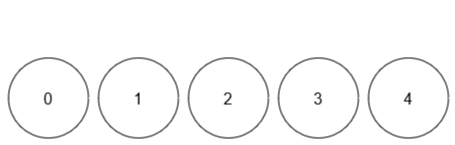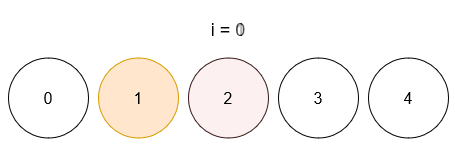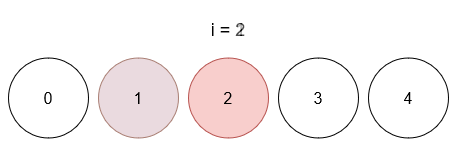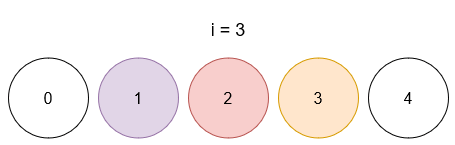
- After query 0, ball 1 has color 4.
- After query 1, ball 1 has color 4, and ball 2 has color 5.
- After query 2, ball 1 has color 3, and ball 2 has color 5.
- After query 3, ball 1 has color 3, ball 2 has color 5, and ball 3 has color 4.
Example 2:
Input: limit = 4, queries = [[0,1],[1,2],[2,2],[3,4],[4,5]]
Output: [1,2,2,3,4]
Explanation:

- After query 0, ball 0 has color 1.
- After query 1, ball 0 has color 1, and ball 1 has color 2.
- After query 2, ball 0 has color 1, and balls 1 and 2 have color 2.
- After query 3, ball 0 has color 1, balls 1 and 2 have color 2, and ball 3 has color 4.
- After query 4, ball 0 has color 1, balls 1 and 2 have color 2, ball 3 has color 4, and ball 4 has color 5.
Constraints:
1 <= limit <= 1091 <= n == queries.length <= 105queries[i].length == 20 <= queries[i][0] <= limit1 <= queries[i][1] <= 109
Solutions
Solution 1: Double Hash Tables
We use a hash table g to record the color of each ball, and another hash table cnt to record the count of each color.
Next, we traverse the array queries. For each query $(x, y)$, we increase the count of color $y$ by $1$, then check whether ball $x$ has been colored. If it has, we decrease the count of the color of ball $x$ by $1$. If the count drops to $0$, we remove it from the hash table cnt. Then, we update the color of ball $x$ to $y$, and add the current size of the hash table cnt to the answer array.
After the traversal, we return the answer array.
The time complexity is $O(m)$, and the space complexity is $O(m)$, where $m$ is the length of the array queries.
-
class Solution { public int[] queryResults(int limit, int[][] queries) { Map<Integer, Integer> g = new HashMap<>(); Map<Integer, Integer> cnt = new HashMap<>(); int m = queries.length; int[] ans = new int[m]; for (int i = 0; i < m; ++i) { int x = queries[i][0], y = queries[i][1]; cnt.merge(y, 1, Integer::sum); if (g.containsKey(x) && cnt.merge(g.get(x), -1, Integer::sum) == 0) { cnt.remove(g.get(x)); } g.put(x, y); ans[i] = cnt.size(); } return ans; } } -
class Solution { public: vector<int> queryResults(int limit, vector<vector<int>>& queries) { unordered_map<int, int> g; unordered_map<int, int> cnt; vector<int> ans; for (auto& q : queries) { int x = q[0], y = q[1]; cnt[y]++; if (g.contains(x) && --cnt[g[x]] == 0) { cnt.erase(g[x]); } g[x] = y; ans.push_back(cnt.size()); } return ans; } }; -
class Solution: def queryResults(self, limit: int, queries: List[List[int]]) -> List[int]: g = {} cnt = Counter() ans = [] for x, y in queries: cnt[y] += 1 if x in g: cnt[g[x]] -= 1 if cnt[g[x]] == 0: cnt.pop(g[x]) g[x] = y ans.append(len(cnt)) return ans -
func queryResults(limit int, queries [][]int) (ans []int) { g := map[int]int{} cnt := map[int]int{} for _, q := range queries { x, y := q[0], q[1] cnt[y]++ if v, ok := g[x]; ok { cnt[v]-- if cnt[v] == 0 { delete(cnt, v) } } g[x] = y ans = append(ans, len(cnt)) } return } -
function queryResults(limit: number, queries: number[][]): number[] { const g = new Map<number, number>(); const cnt = new Map<number, number>(); const ans: number[] = []; for (const [x, y] of queries) { cnt.set(y, (cnt.get(y) ?? 0) + 1); if (g.has(x)) { const v = g.get(x)!; cnt.set(v, cnt.get(v)! - 1); if (cnt.get(v) === 0) { cnt.delete(v); } } g.set(x, y); ans.push(cnt.size); } return ans; }